【题目】如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①△DEF是等腰直角三角形;
②AE=CF;
③△BDE≌△ADF;
④BE+CF=EF;
⑤S四边形AEDF=![]() AD2,
AD2,
其中正确结论是_____(填序号)

参考答案:
【答案】①②③
【解析】
先由ASA证明△AED≌△CFD,得出AE=CF,DE=FD;再由全等三角形的性质得到BE+CF=AB,由勾股定理求得EF与AB的值,通过比较它们的大小来判定④的正误;先得出S四边形AEDF=S△ADC=![]() AD2,从而判定⑤的正误.
AD2,从而判定⑤的正误.
解:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,
∵∠MDN=90°,
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF,ED=FD.故①②正确;
又∵△ABD≌△ACD,
∴△BDE≌△ADF.故③正确;
∵△AED≌△CFD,
∴AE=CF,ED=FD,
∴BE+CF=BE+AE=AB=![]() BD,
BD,
∵EF=![]() ED,BD>ED,
ED,BD>ED,
∴BE+CF>EF.故④错误;
∵△AED≌△CFD,△BDE≌△ADF,
∴S四边形AEDF=S△ADC=![]() AD2.故⑤错误.
AD2.故⑤错误.
综上所述,正确结论是①②③.
故答案是:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣  x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,CA=12
 cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2  cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
(1)∠CAB的度数是;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形ABC在平面直角坐标系中的位置如图所示.将三角形ABC向右平移6个单位长度,再向下平移6个单位长度得到三角形A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的三角形A1B1C1;
(2)求三角形ABC的面积;
(3)直接写出三角形A1B1C1各顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商城销售
 、
、 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为 元、
元、 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:销售时段
销售型号
销售收入
 种型号
种型号 种型号
种型号第一周
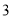 台
台 台
台 元
元第二周
 台
台 台
台 元
元(1)求
 、
、 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;(2)若商城准备用不多于
 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共 台,求
台,求 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?(3)在(2)的条件下商城销售完这
 台电风能否实现利润超过
台电风能否实现利润超过 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
相关试题

