搜索
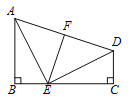
【题目】如图：AB⊥BC，DC⊥BC，E在BC上，AB＝EC，BE＝CD，EF⊥AD于F.
(1)求证：F是AD中点；
(2)求∠AEF的度数.
参考答案：
【答案】（1）证明见解析；（2）45°
【解析】试题分析：（1）由题意，AB⊥BC，DC⊥BC，AB=EC，BE=CD，可证△ABE≌△ECD，可证AE=ED，且EF⊥AD，即可得证F是AD是中点．
（2）由（1）可推出，△AED为等腰直角三角形，所以∠AEF=45°．
试题解析：由题意，AB⊥BC，DC⊥BC，AB=EC，BE=CD，
所以△ABE≌△ECD，
所以AE=ED，
又EF⊥AD，
即可得证F是AD是中点；
（2）由（1）得，∠AEB+∠CED=90°；
所以∠AED=90°，
所以△AED为等腰直角三角形，
所以∠AEF=45°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=﹣
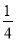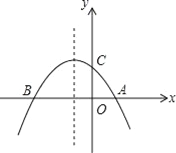
x2﹣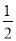
x+2与x轴交于A、B两点，与y轴交于点C（1）求点A，B，C的坐标；
（2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；
（3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC，其中正确结论的个数是（ ）．
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E、F，连接EF．
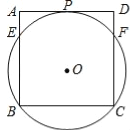
（1）求证：PF平分∠BFD．
（2）若tan∠FBC=
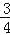，DF=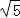
，求EF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知正比例函数y＝（m﹣1）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是（ ）
A. m＜1B. m＞1C. m＜2D. m＞0
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题4分）（1）在图1中， 求∠A1＋∠B1＋∠C1＋∠A2＋∠B2＋∠C2的度数= ．
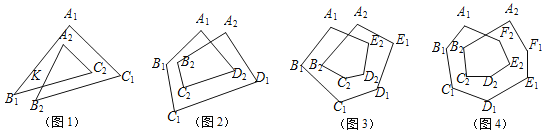
（2）我们作如下规定：
图1称为2环三角形，它的内角和为∠A1＋∠B1＋∠C1＋∠A2＋∠B2＋∠C2；
图2为2环四边形，它的内角和为∠A1＋∠B1＋∠C1＋∠D1＋∠A2＋∠B2＋∠C2＋∠D2；
图3称为2环5五边形，它的内角和为∠A1＋∠B1＋∠C1＋∠D1＋∠E1＋∠A2＋∠B2＋∠C2＋∠D2＋∠E2；
想一想：2环n边形的内角和为 度（只要求直接写出结论）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．
（1）求证：△ABE≌△CAD；
（2）求∠AFE的度数．
相关试题
