【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠AFE的度数.

参考答案:
【答案】(1)证明详见解析;(2)60°.
【解析】
试题分析:(1)根据等边三角形的性质可得,∠BAC=∠C=60°,AB=CA,然后利用“边角边”证明△ABE和△CAD全等;
(2)根据全等三角形对应角相等可得∠ABE=∠CAD,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理得到∠AFE=∠BAC.
试题解析:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA,
即∠BAE=∠C=60°,
在△ABE和△CAD中,
AB=CA,∠BAC=∠C,AE=CD,
∴△ABE≌△CAD(SAS);
(2)解:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠AFE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°.
-
科目: 来源: 题型:
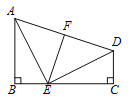
查看答案和解析>>【题目】如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F.
(1)求证:F是AD中点;
(2)求∠AEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=(m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A. m<1B. m>1C. m<2D. m>0
-
科目: 来源: 题型:
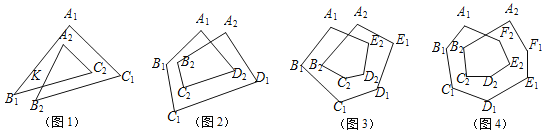
查看答案和解析>>【题目】(本小题4分)(1)在图1中, 求∠A1+∠B1+∠C1+∠A2+∠B2+∠C2的度数= .
(2)我们作如下规定:
图1称为2环三角形,它的内角和为∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1+∠A2+∠B2+∠C2+∠D2+∠E2;
想一想:2环n边形的内角和为 度(只要求直接写出结论).
-
科目: 来源: 题型:
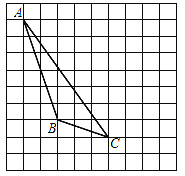
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)利用网格点和直尺画图:画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,点E是异于A点的格点,则这样的E点有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟内它从原点运动到(1,0),而后它接着按图示在x轴、y轴平行的方向上来回运动,且每分钟移动一个长度单位,那么在2015分钟后这个粒子所处的位置(坐标)是 ______ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A. 掷一块石块,石块下落
B. 射击运动员射击一次,命中10环
C. 随意掷一块质地均匀的骰子,掷出的点数是1
D. 在一个装满白球和黑球的袋中摸球,摸出红球
相关试题

