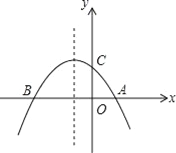
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)点A坐标(2,0),点B坐标(﹣4,0),点C坐标(0,2);(2)![]() ;(3)M坐标为(﹣1,﹣1)或(﹣1,2+
;(3)M坐标为(﹣1,﹣1)或(﹣1,2+![]() )或(﹣1.2﹣
)或(﹣1.2﹣![]() ).
).
【解析】试题分析:(1)分别令y=0,x=0,即可解决问题.
(2)由图象可知AB只能为平行四边形的边,易知点E坐标,由此不难解决问题.
(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.
试题解析:(1)令y=0得![]() ,∴
,∴![]() ,x=﹣4或2,∴点A坐标(2,0),点B坐标(﹣4,0),令x=0,得y=2,∴点C坐标(0,2).
,x=﹣4或2,∴点A坐标(2,0),点B坐标(﹣4,0),令x=0,得y=2,∴点C坐标(0,2).
(2)由图象可知AB只能为平行四边形的边,∵AB=EF=6,对称轴x=﹣1,∴点E的横坐标为﹣7或5,∴点E坐标(﹣7, ![]() )或(5,
)或(5, ![]() ),此时点F(﹣1,
),此时点F(﹣1, ![]() ),∴以A,B,E,F为顶点的平行四边形的面积=6×
),∴以A,B,E,F为顶点的平行四边形的面积=6×![]() =
=![]() .
.
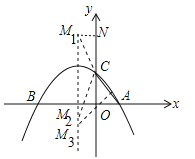
(3)如图所示,①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,在RT△CM1N中,CN=![]() =
=![]() ,∴点M1坐标(﹣1,
,∴点M1坐标(﹣1, ![]() ),点M2坐标(﹣1,
),点M2坐标(﹣1, ![]() ).
).
②当M3为顶点时,∵直线AC解析式为y=﹣x+1,线段AC的垂直平分线为y=x,∴点M3坐标为(﹣1,﹣1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1, ![]() )或(﹣1,
)或(﹣1, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;④AD∥BE;且∠BAD=∠BCD.其中,能推出AB∥DC的条件为________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽6名同学参加体能测试,成绩分别是80,90,75,75,80,80.则这组同学的测试成绩的中位数是( )
A. 75B. 80C. 85D. 90
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1、2、5、3、5、3、3的中位数是
A. 1 B. 2 C. 3 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB、AC为一边,向外作正方形ABDE和ACFG,连接CE、BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( ).

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
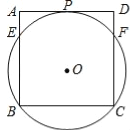
(1)求证:PF平分∠BFD.
(2)若tan∠FBC=
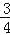 ,DF=
,DF=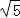 ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
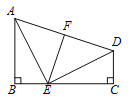
查看答案和解析>>【题目】如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F.
(1)求证:F是AD中点;
(2)求∠AEF的度数.
相关试题

