搜索
【题目】如图，CD是线段AB的垂直平分线，则∠CAD=∠CBD.请说明理由：
证明∵ CD是线段AB的垂直平分线（已知）
∴AC=BC， =BD
（ ）.
在△ACD和△BCD中，
∴△ACD≌△BCD（SSS ）.
∴ ∠CAD=∠CBD（ ）.
参考答案：
【答案】答案见解析
【解析】试题分析：根据线段垂直平分线性质得出AC=BC，AD=BD，根据SSS证出△CBD≌△CAD即可．
试题解析：解：∵ CD是线段AB的垂直平分线（已知）
∴AC=BC， AD =BD（ 线段垂直平分线上的点到线段两个端点的距离相等）．
在△ACD和△BCD中，
，
AD= BD （已证），
CD=CD （ 公共边 ），
∴△ACD≌△BCD（SSS ）．
∴ ∠CAD=∠CBD（ 全等三角形的对应角相等 ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知2y2+y﹣2的值为3，则4y2+2y+1的值为（ ）
A.10
B.11
C.10或11
D.3或11 -
科目： 来源： 题型：
查看答案和解析>>【题目】为培养学生养成良好的“爱读书，读好书，好读书”的习惯，我市某中学举办了“汉字听写大赛”，准备为获奖同学颁奖．在购买奖品时发现，一个书包和一本词典会花去48元，用124元恰好可以购买3个书包和2本词典．
（1）每个书包和每本词典的价格各是多少元？
（2）学校计划总费用不超过900元,为获胜的40名同学颁发奖品（每人一个书包或一本词典），求最多可以购买多少个书包？
-
科目： 来源： 题型：
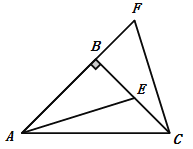
查看答案和解析>>【题目】如图,在△ABC中,AB=BC, ∠ABC=90°,F为AB 延长线上的一点,点E在BC上,且AE=CF.
(1)求证: △ABE≌△CBF.
(2)若∠CAE=15°,求∠ACF的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式
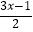﹣1≤ 
，并把解集在数轴上表示出来． -
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式组：
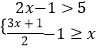，并在数轴上表示出不等式组的解集． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示.
乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元.
（1）求如图所示的y与x的函数解析式；（不要求写取值范围）
（2）如果某学校目前的绿化面积是1200平方米.试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少.
相关试题
