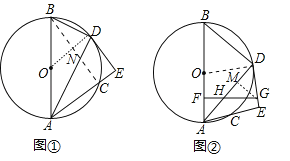
【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=![]() ,tan∠BAD=
,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)4.
;(3)4.
【解析】试题分析:(1)欲证明DE是⊙O的切线,只要证明OD⊥DE;
(2)首先证明OD⊥BC,在Rt△BDN中,利用勾股定理计算即可;
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,想办法用x表示线段FH、GH,根据FH+GH=
x,想办法用x表示线段FH、GH,根据FH+GH=![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
试题解析:解:(1)证明:如图①中,连接OD.∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠DAE,∴∠ODA=∠DAE,∴OD∥AE,∴∠ODE+∠AED=180°,∵∠AED=90°,∴∠ODE=90°,∴OD⊥DE,∴DE是⊙O的切线.
(2)如图①中,连接BC,交OD于点N,∵AB是直径,∴∠BCA=90°,∵OD∥AE,O是AB的中点,∴ON∥AC,且ON=![]() AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=
AC,∴∠ONB=90°,且ON=3,则BN=4,ND=2,∴BD=![]() =
=![]() .
.
(3)如图②中,设FG与AD交于点H,根据题意,设AB=5x,AD=4x,则AF=![]() x,FH=AFtan∠BAD=
x,FH=AFtan∠BAD=![]() x
x![]() =
=![]() x,AH=
x,AH=![]() =
=![]() =
=![]() ,HD=AD﹣AH=4x﹣
,HD=AD﹣AH=4x﹣![]() =
=![]() ,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=
,由(1)可知,∠HDG+∠ODA=90°,在Rt△HFA中,∠FAH+∠FHA=90°,∵∠OAD=∠ODA,∠FHA=∠DHG,∴∠DHG=∠HDG,∴GH=GD,过点G作GM⊥HD,交HD于点M,∴MH=MD,∴HM=![]() HD=
HD=![]() ×
×![]() =
=![]() ,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=
,∵∠FAH+∠AHF=90°,∠MHG+∠HGM=90°,∴∠FAH=∠HGM,在Rt△HGM中,HG=![]() =
=![]() =
=![]() ,∵FH+GH=
,∵FH+GH=![]() ,∴
,∴![]() +
+![]() =
=![]() ,解得x=
,解得x=![]() ,∴此圆的半径为
,∴此圆的半径为![]() ×
×![]() =4.
=4.
-
科目: 来源: 题型:
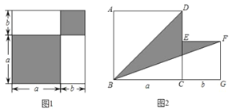
查看答案和解析>>【题目】请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: .
方法2: .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:如图2,两个正方形边长分别为a、b,如果a+b=10,ab=21,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)
(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为__________.
(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由。
(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,
 ,点E、F分别在边AD和边BC上,且
,点E、F分别在边AD和边BC上,且 ,动点P、Q分别从A、C两点同时出发,点P自A→F→B方向运动,点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s,3cm/s,设运动时间为
,动点P、Q分别从A、C两点同时出发,点P自A→F→B方向运动,点Q自C→D→E→C方向运动若点P、Q的运动速度分别为1cm/s,3cm/s,设运动时间为 ,当A 、C、P、Q四点为顶点的四边形是平行四边形时则t= ________________
,当A 、C、P、Q四点为顶点的四边形是平行四边形时则t= ________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级
中位数(分)
众数(分)
平均数(分)
爱国班
85
求知班
100
85
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?

相关试题

