【题目】如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
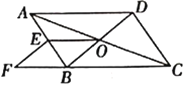
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是矩形?并说明理由;
是矩形?并说明理由;
(3)当线段![]() 和
和![]() 之间满足什么条件时,四边形
之间满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)首先证明OE是△ABC的中位线,推出OE∥BC,由EF∥OB,推荐可提出四边形OBFE是平行四边形.
(2)当AD⊥BD时,四边形OBFE是矩形.只要证明∠EOB=90°即可解决问题;
(3)当AD⊥BD,AD=BD时,四边形OBFE是正方形.根据中位线性质再证OB=OE即可.
(1)证明:∵四边形ABCD是平行四边形,
∴点O是AC的中点.
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF.
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形.

(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD,AD=BD时,四边形OBFE是正方形.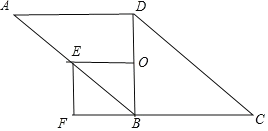
理由:∵OE为△ABD的中位线,
∴OE=![]() AD
AD
∵O为BD中点,
∴OB=![]() BD,
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD,AD=BD时,四边形OBFE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2
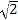 ,求BD的长.
,求BD的长.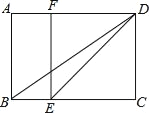
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在笔直的公路
 旁有一座山,为方便运输货物现要从公路
旁有一座山,为方便运输货物现要从公路 上的
上的 处开凿隧道修通一条公路到
处开凿隧道修通一条公路到 处,已知点
处,已知点 与公路上的停靠站
与公路上的停靠站 的距离为
的距离为 ,与公路上另-停靠站
,与公路上另-停靠站 的距离为
的距离为 ,停靠站
,停靠站 之间的距离为
之间的距离为 ,且
,且
 求修建的公路
求修建的公路 的长;
的长; 若公路
若公路 修通后,辆货车从
修通后,辆货车从 处经过
处经过 点到
点到 处的路程是多少?
处的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与运用观察发现:解方程组
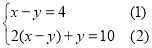 ,将(1)整体代入(2),得2×4+y=10,解得y=2,把y=2代入(1),得x=6,所以
,将(1)整体代入(2),得2×4+y=10,解得y=2,把y=2代入(1),得x=6,所以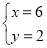 ;这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答.已知关于a、b的方程组:
;这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答.已知关于a、b的方程组: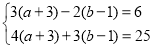 .
.(1)求a+b的值;
(2)若关于x的不等式组
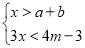 恰好有1个整数解,求m的取值范围.
恰好有1个整数解,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,按如下步骤作图: ①分别以点B、C为圆心,大于
 AB的长为半径作弧,两弧相交于点M和N;
AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 .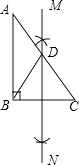
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC经过平移之后成为△DEF,那么:
(1)点A的对应点是点________;
(2)点________的对应点是点F;
(3)线段AB的对应线段是线段________;
(4)线段BC的对应线段是线段________;
(5)∠A的对应角是________;
(6)________的对应角是∠F.

相关试题

