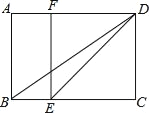
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
(1)先证明四边形FECD为平行四边形,再证出CD=CE,得出四边形FECD为菱形,由∠C=90°,即可得出四边形FECD为正方形;
(2)先由三角函数求出正方形FECD的边长CD=CE,得出BC,进而得出BD的长.
(1)∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=∠C=90°,
∵EF∥DC,
∴四边形FECD为平行四边形,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠DEC,
∴∠CDE=∠DEC,
∴CD=CE,
∴四边形FECD是菱形,
又∵∠C=90°,
∴平行四边形FECD是正方形;
(2)∵四边形FECD是正方形,
∴∠CDE=45°,
∵ED=2![]() ,
,
∴CE=CD=EDsin45°=2![]() ×
×![]() =2,
=2,
∴BC=BE+EC=1+2=3,
∴BD2=BC2+CD2=32+22=13,
∴BD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,
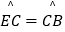 .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 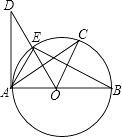
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校“阳光体育”活动的开展情况,从该校1000名学生中随机抽取部分学生进行问卷调查(每名学生只能填写一项自己最喜欢的体育项目),并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中信息,解答下列问题:
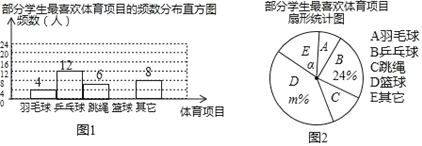
(1)被调查的学生共有多少人?
(2)扇形统计图中m的值和a的度数分别是多少?
(3)根据部分学生最喜欢体育项目的调查情况,请估计全校学生中最喜欢篮球的人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫.已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨.
(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?
(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在笔直的公路
 旁有一座山,为方便运输货物现要从公路
旁有一座山,为方便运输货物现要从公路 上的
上的 处开凿隧道修通一条公路到
处开凿隧道修通一条公路到 处,已知点
处,已知点 与公路上的停靠站
与公路上的停靠站 的距离为
的距离为 ,与公路上另-停靠站
,与公路上另-停靠站 的距离为
的距离为 ,停靠站
,停靠站 之间的距离为
之间的距离为 ,且
,且
 求修建的公路
求修建的公路 的长;
的长; 若公路
若公路 修通后,辆货车从
修通后,辆货车从 处经过
处经过 点到
点到 处的路程是多少?
处的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与运用观察发现:解方程组
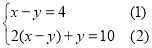 ,将(1)整体代入(2),得2×4+y=10,解得y=2,把y=2代入(1),得x=6,所以
,将(1)整体代入(2),得2×4+y=10,解得y=2,把y=2代入(1),得x=6,所以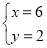 ;这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答.已知关于a、b的方程组:
;这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此方法解答.已知关于a、b的方程组: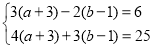 .
.(1)求a+b的值;
(2)若关于x的不等式组
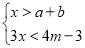 恰好有1个整数解,求m的取值范围.
恰好有1个整数解,求m的取值范围. -
科目: 来源: 题型:
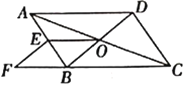
查看答案和解析>>【题目】如图,在
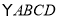 中,对角线
中,对角线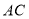 ,
,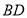 交于点
交于点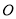 ,
,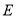 为
为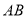 的中点,点
的中点,点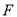 在
在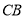 的延长线上,且
的延长线上,且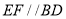 .
.
(1)求证:四边形
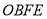 是平行四边形;
是平行四边形;(2)当线段
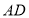 和
和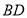 之间满足什么条件时,四边形
之间满足什么条件时,四边形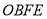 是矩形?并说明理由;
是矩形?并说明理由;(3)当线段
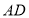 和
和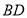 之间满足什么条件时,四边形
之间满足什么条件时,四边形 是正方形?并说明理由.
是正方形?并说明理由.
相关试题

