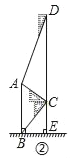
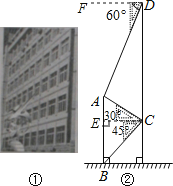
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

参考答案:
【答案】雕塑AB的高度约为6.8米.
【解析】试题分析:首先证明△ADC是直角三角形,求出AC.在Rt△ACE中,求出AE.在Rt△BCE中,求出BE,即可解决问题.
试题解析:解:过点C作CE⊥AB于E.∵∠ADC=90°﹣60°=30°,∠ACD=90°﹣30°=60°,∴∠CAD=90°.∵CD=10,∴AC=![]() CD=5.
CD=5.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,∴AE=![]() AC=
AC=![]() ,CE=ACcos∠ACE=5cos30°=
,CE=ACcos∠ACE=5cos30°=![]() .
.
在Rt△BCE中,∵∠BCE=45°,∴BE=CE=![]() ,∴AB=AE+BE=
,∴AB=AE+BE=![]() +
+![]() =
=![]() (
( ![]() +1)≈6.8(米).
+1)≈6.8(米).
答:雕塑AB的高度约为6.8米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,反比例函数y=
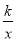 (x>0),过点A(3,4).
(x>0),过点A(3,4).(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料
如图1,若线段
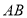 在数轴上,
在数轴上,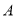 、
、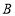 两点表示的数分别是
两点表示的数分别是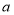 ,
,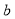
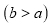 ,则线段
,则线段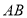 的长(点
的长(点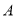 到点
到点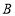 的距离)可表示为
的距离)可表示为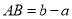 .
.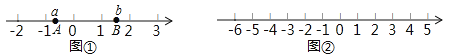
请用上面的材料中的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动2个单位长度到达
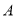 点,再向右移动7个单位长度到达
点,再向右移动7个单位长度到达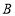 点.
点.(1)此时点
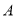 在数轴上表示的数为 ;点
在数轴上表示的数为 ;点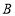 在数轴上表示的数为 ;并在图②中表示出
在数轴上表示的数为 ;并在图②中表示出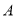 、
、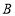 两点的位置.
两点的位置.(2)若将点
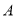 向左移动
向左移动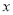 个单位长度,则移动后点
个单位长度,则移动后点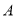 表示为 (用含
表示为 (用含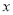 的代数式表示)
的代数式表示)(3)若点
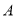 以每秒2个单位长度的速度沿数轴向右匀速移动,同时,点
以每秒2个单位长度的速度沿数轴向右匀速移动,同时,点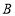 以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为
以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为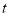 秒,则当
秒,则当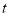 为何值时
为何值时 .
.(4)若点
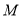 从原点
从原点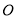 出发以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为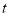 秒,同时,另一点
秒,同时,另一点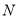 从点
从点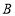 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,到达原点
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,到达原点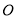 后立即原路返回向右运动,当
后立即原路返回向右运动,当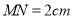 时,画出图形并求出时间
时,画出图形并求出时间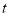 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中
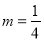 ,n=-1.”小强不小心把
,n=-1.”小强不小心把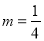 错抄成了
错抄成了 ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果
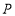 处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
A.10010B.10101
C.10100D.10110
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某勘测队在一条近似笔直的河流l两边勘测(河宽忽略不计),共设置了A,B,C三个勘测点.
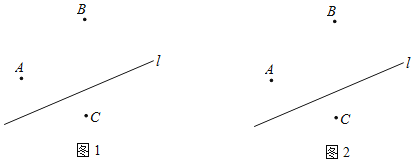
(1)若勘测队在A点建一水池,现将河水引入到水池A中,则在河岸的什么位置开沟,才能使水沟的长度最短?请在图1中画出图形;你画图的依据是 .
(2)若勘测队在河岸某处开沟,使得该处到勘测点B,C所挖水沟的长度之和最短,请在图2中画出图形;你画图的依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)和点B,化简
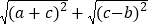 的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )
的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )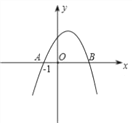
A. 一个 B. 两个 C. 三个 D. 四个
相关试题

