【题目】阅读下面材料
如图1,若线段![]() 在数轴上,
在数轴上,![]() 、
、![]() 两点表示的数分别是
两点表示的数分别是![]() ,
,![]()
![]() ,则线段
,则线段![]() 的长(点
的长(点![]() 到点
到点![]() 的距离)可表示为
的距离)可表示为![]() .
.
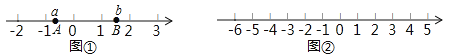
请用上面的材料中的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动2个单位长度到达![]() 点,再向右移动7个单位长度到达
点,再向右移动7个单位长度到达![]() 点.
点.
(1)此时点![]() 在数轴上表示的数为 ;点
在数轴上表示的数为 ;点![]() 在数轴上表示的数为 ;并在图②中表示出
在数轴上表示的数为 ;并在图②中表示出![]() 、
、![]() 两点的位置.
两点的位置.
(2)若将点![]() 向左移动
向左移动![]() 个单位长度,则移动后点
个单位长度,则移动后点![]() 表示为 (用含
表示为 (用含![]() 的代数式表示)
的代数式表示)
(3)若点![]() 以每秒2个单位长度的速度沿数轴向右匀速移动,同时,点
以每秒2个单位长度的速度沿数轴向右匀速移动,同时,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为
以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒,则当
秒,则当![]() 为何值时
为何值时![]() .
.
(4)若点![]() 从原点
从原点![]() 出发以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发以每秒1个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒,同时,另一点
秒,同时,另一点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,到达原点
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,到达原点![]() 后立即原路返回向右运动,当
后立即原路返回向右运动,当![]() 时,画出图形并求出时间
时,画出图形并求出时间![]() 的值.
的值.
参考答案:
【答案】(1)点![]() 表示的数为-2;点
表示的数为-2;点![]() 表示的数为5;数轴表示见解析;(2)点
表示的数为5;数轴表示见解析;(2)点![]() 表示为-2-
表示为-2-![]() ;;(3)t =1秒或1.8秒;(4)t=1秒或t=
;;(3)t =1秒或1.8秒;(4)t=1秒或t=![]() 秒或t=3秒或t=7秒时.
秒或t=3秒或t=7秒时.
【解析】
(1)根据左减右加可以得到移动后A、B点表示的数;
(2)根据左减右加可以得到移动后A点表示的数;
(3)先表示移动后A、B点表示的数,再分两种情况讨论![]() ,列方程求解即可;
,列方程求解即可;
(4)先求出点N到达原点O的时间,以这个时间为界分两种情况讨论求解.
解:(1)点![]() 在数轴上表示的数为0-2=-2;
在数轴上表示的数为0-2=-2;
点![]() 在数轴上表示的数为-2+7=5;
在数轴上表示的数为-2+7=5;
点![]() 点
点![]() 位置如图所示:
位置如图所示: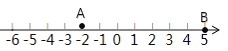
(2)将点![]() 向左移动
向左移动![]() 个单位长度,则移动后点
个单位长度,则移动后点![]() 表示为-2-
表示为-2-![]() ;;
;;
(3)运动时间为![]() 秒时,
秒时,
点A向右移动了2t个单位,则移动后的点A表示的数为-2+2t;
点B向左移动了3t个单位,则移动后的点B表示的数为5-3t;
分两种情况讨论:
当点A在点B左边时,
∵AB=2,
∴(5-3t)-( -2+2t) =2,
解得:t =1;
当点A在点B右边时,
∵AB=2,
∴( -2+2t) -(5-3t) =2,
解得:t =1.8;
综上所述,当t =1秒或1.8秒时AB=2;
(4)运动时间为![]() 秒时,
秒时,
点M向右移动了t个单位,则移动后的点M表示的数为t;
当t=2.5秒时,点N到原点O;
当t![]() 2.5秒时,点N向左移动了2t个单位,则移动后的点N表示的数为5-2t;
2.5秒时,点N向左移动了2t个单位,则移动后的点N表示的数为5-2t;
当t>2.5秒时,点N从原点向右移动了(2t-5)个单位,则移动后的点N表示的数为2t-5;
下面分两种情况讨论:
如图③,当t![]() 2.5秒时,MN=2,
2.5秒时,MN=2,
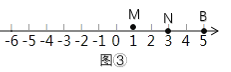
则(5-2t)- t=2或t-(5-2t)=2,
解得t=1或t=![]() ;
;
如图④⑤,当t>2.5秒时,MN=2,
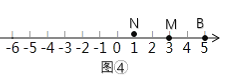
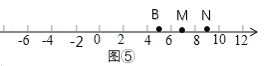
则t-(2t-5)=2 或(2t-5)- t=2,
解得t=3或t=7;
综上所述,当t=1秒或t=![]() 秒或t=3秒或t=7秒时,MN=2.
秒或t=3秒或t=7秒时,MN=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号
1
2
3
4
5
6
正方形个数
1
4
7
10
_____
_____
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,反比例函数y=
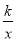 (x>0),过点A(3,4).
(x>0),过点A(3,4).(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中
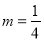 ,n=-1.”小强不小心把
,n=-1.”小强不小心把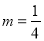 错抄成了
错抄成了 ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗? -
科目: 来源: 题型:
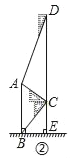
查看答案和解析>>【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
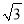 =1.73).
=1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果
 处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
A.10010B.10101
C.10100D.10110
相关试题

