【题目】某校准备组织七年级400名学生参加北京夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人;用1辆小客车和2辆大客车每次可运送学生110人;
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满;
①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
参考答案:
【答案】(1)每辆小客车能坐20名学生, 每辆大客车能坐45名学生.(2)租车方案有3种.方案1:小客车20辆,大客车0辆;方案2:小客车11辆,大客车4辆;方案3:小客车2辆,大客车8辆. 68800元
【解析】
(1)设1辆小客车一次可送学生a人,1辆大客车都坐满后一次可送b名学生,根据题意可得等量关系:①用3辆小客车拉的人数+1辆大客车拉的人数=运送学生105人;②用1辆小客车拉的人数+2辆大客车拉的人数=运送学生110人,根据等量关系列出方程组,再解即可;
(2)由题意得:20×小客车的数量+45×大客车的数量=400人,根据等量关系列出方程,求出非负整数解即可;
(3)分别计算出每种租车方案的钱数,进行比较即可.
(1)设每辆小客车能坐a名学生, 每辆大客车能坐b名学生
根据题意,得
![]()
解得![]()
答: 每辆小客车能坐20名学生, 每辆大客车能坐45名学生.
(2)①根据题意,得20x+45y=400,
∴![]() ,
,
∵x、y均为非负数,
∴![]()
∴租车方案有3种.方案1:小客车20辆,大客车0辆;方案2:小客车11辆,大客车4辆;方案3:小客车2辆,大客车8辆.
②方案1租金:4000×20=80000(元)
方案2租金:4000×11+7600×4=74400(元)
方案3租金:4000×2+7600×8=68800(元)
∵80000>74400>68800
∴方案3租金最少,最少租金为68800元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组)
(1)

(2)

(3)

(4)9(3x+2)2﹣64=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某牧区需要550顶帐篷过冬,现由甲、乙两个工厂生产,已知甲工厂每天生产的能力是乙工厂的1.5倍,并且生产240顶帐篷甲工厂比乙工厂少4天,
(1)甲、乙两个工厂每天分别生产多少顶帐篷?
(2)若甲工厂每天生产成本为3万元,乙工厂每天生产成本为2.4万元,要使这批帐篷的生产总成本不高于60万元,至少应安排甲工厂生产多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD=
 AM2.
AM2.其中正确结论的个数是( )
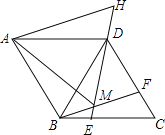
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a、b都是实数,且满足2a﹣b=6,就称点P
 为完美点.
为完美点.(1)判断点A(2,3)是否为完美点?
(2)完美点一定不在第 象限;
(3)已知关于m、n的方程组
 ,当t为何值时,以方程组的解为坐标的点B是完美点,请说明理由.
,当t为何值时,以方程组的解为坐标的点B是完美点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

相关试题

