【题目】如图(1),∠AOB=120°,在∠AOB内作两条射线OC和OD,且OM平分∠AOD,ON平分∠BOC.
①若∠AOC:∠COD:∠DOB=5:3:4,求∠MON的度数.
②若将图(1)中的∠COD绕点O顺时针转一个小于70°的角α如图(2),其它条件不变,请直接写出∠MON的度数.

参考答案:
【答案】(1)45°;(2)45°.
【解析】试题分析:(1)先根据∠AOC:∠COD:∠DOB=5:3:4,设∠AOC=5x,∠COD=3x,∠DOB=4x,再根据∠AOC+∠COD+∠BOD=120°,列出方程5x+3x+4x=120°,求得x的值后,得出∠AOC=50°,∠COD=30°,∠DOB=40°,再根据∠MON=∠DOM+∠CON-∠COD进行计算,即可∠MON的度数;
(2)先根据OM平分∠AOD,ON平分∠BOC,得出∠DOM=![]() ∠AOD,∠CON=
∠AOD,∠CON=![]() ∠BOC,再根据∠MON=∠DOM+∠CON-∠COD=
∠BOC,再根据∠MON=∠DOM+∠CON-∠COD=![]() ∠AOD+
∠AOD+![]() ∠BOC-∠COD=
∠BOC-∠COD=![]() (∠AOD+∠BOC)-∠COD=
(∠AOD+∠BOC)-∠COD=![]() (∠AOB+∠COD)-∠COD进行计算,即可得出∠MON的度数.
(∠AOB+∠COD)-∠COD进行计算,即可得出∠MON的度数.
试题解析:(1)如图,

∵∠AOC:∠COD:∠DOB=5:3:4,
∴可设∠AOC=5x,∠COD=3x,∠DOB=4x,
∵∠AOB=120°,
∴∠AOC+∠COD+∠BOD=120°,
∴5x+3x+4x=120°,
解得x=10°,
∴∠AOC=50°,∠COD=30°,∠DOB=40°,
∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=![]() ∠AOD=
∠AOD=![]() (50°+30°)=40°,
(50°+30°)=40°,
∠CON=![]() ∠BOC=
∠BOC=![]() (30°+40°)=35°,
(30°+40°)=35°,
∴∠MON=∠DOM+∠CON﹣∠COD=40°+35°﹣30°=45°;
(2)如图,

∵OM平分∠AOD,ON平分∠BOC,
∴∠DOM=![]() ∠AOD,∠CON=
∠AOD,∠CON=![]() ∠BOC,
∠BOC,
∴∠MON=∠DOM+∠CON﹣∠COD
=![]() ∠AOD+
∠AOD+![]() ∠BOC﹣∠COD
∠BOC﹣∠COD
=![]() (∠AOD+∠BOC)﹣∠COD
(∠AOD+∠BOC)﹣∠COD
=![]() (∠AOB+∠COD)﹣∠COD
(∠AOB+∠COD)﹣∠COD
=![]() ∠AOB﹣
∠AOB﹣![]() ∠COD
∠COD
=![]() ×120°﹣
×120°﹣![]() ×30°
×30°
=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某工厂产值连续增长,去年是前年的1.5倍,今年是去年的2倍,这三年的总产值为550万元,问前年的产值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx﹣4,当x=2时,y=﹣2.
(1)求此一次函数的解析式;
(2)将该函数的图象向上平移3个单位,求平移后的图象与x轴的交点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.
求证:DE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
 ;
;(2)
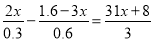 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.

(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】物体向右运动4m记作+4m,那么物体向左运动3m,应记作m.
相关试题

