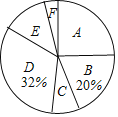
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分.
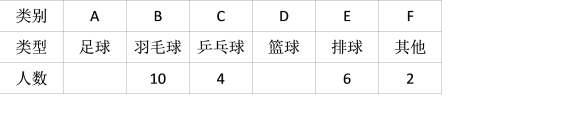
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜欢乒乓球的有 人,最喜欢篮球的学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,其中,最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %;
(3)该校共有450名学生,根据调查结果,估计该校最喜欢排球的学生数.
参考答案:
【答案】(1)4;32;(2)50;16;24;(3)根据调查结果,估计该校最喜欢排球的学生数为54人.
【解析】(1)依据统计图表中的数据即可得到结果;
(2)依据最喜欢羽毛球的学生数以及占被调查总人数的百分比,即可得到被调查总人数,进而得出最喜欢篮球的学生数以及最喜欢足球的学生数占被调查总人数的百分比;
(3)依据最喜欢排球的学生数占被调查总人数的百分比,即可估计该校最喜欢排球的学生数.
(1)由题可得:被调查的学生中,最喜欢乒乓球的有4人,最喜欢篮球的学生数占被调查总人数的百分比为32%.
故答案为:4;32;
(2)被调查学生的总数为10÷20%=50人,最喜欢篮球的有50×32%=16人,最喜欢足球的学生数占被调查总人数的百分比=![]() ×100%=24%;
×100%=24%;
故答案为:50;16;24;
(3)根据调查结果,估计该校最喜欢排球的学生数为![]() ×450=54人.
×450=54人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,发生的概率是
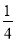 的是( )
的是( )A.从一副扑克牌中,任意抽取其中的一张,抽到红桃的概率
B.一个圆盘被染成红、黄、蓝、紫四种颜色,随机转动一次,转盘停止时,指针刚好指向红色的概率
C.小明开车到十字路口时,遇到红灯的概率
D.一道单选题有
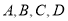 四个备用选项, 从中随机选一个作答,答对的概率
四个备用选项, 从中随机选一个作答,答对的概率 -
科目: 来源: 题型:
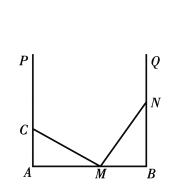
查看答案和解析>>【题目】在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“
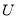 ”字形框架
”字形框架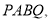 其中
其中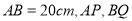 足够长,
足够长,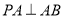 于点
于点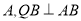 于点
于点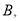 点
点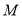 从
从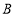 出发向
出发向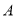 运动,点
运动,点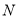 从
从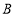 出发向
出发向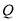 运动, 速度之比为
运动, 速度之比为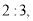 运动到某一瞬间两点同时停止,在
运动到某一瞬间两点同时停止,在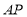 上取点
上取点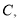 使
使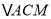 与
与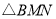 全等,则
全等,则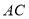 的长度为________________
的长度为________________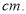
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
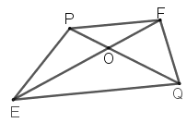
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
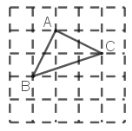
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
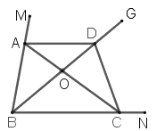
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
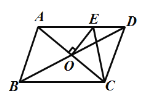
A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
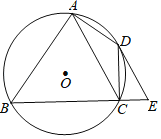
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
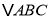 中,
中,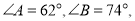 请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.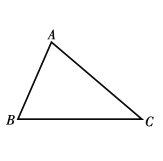
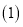 作出
作出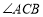 的平分线交
的平分线交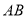 于点
于点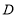 ;
;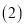 作
作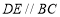 交
交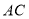 于点
于点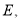 平行依据是_____ __;
平行依据是_____ __;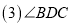 的度数为 .
的度数为 .
相关试题

