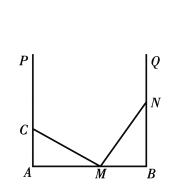
【题目】在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“![]() ”字形框架
”字形框架![]() 其中
其中![]() 足够长,
足够长,![]() 于点
于点![]() 于点
于点![]() 点
点![]() 从
从![]() 出发向
出发向![]() 运动,点
运动,点![]() 从
从![]() 出发向
出发向![]() 运动, 速度之比为
运动, 速度之比为![]() 运动到某一瞬间两点同时停止,在
运动到某一瞬间两点同时停止,在![]() 上取点
上取点![]() 使
使![]() 与
与![]() 全等,则
全等,则![]() 的长度为________________
的长度为________________![]()
参考答案:
【答案】![]() 或
或![]()
【解析】
设点M的速度为2x,点N的速度为3x,运动时间为t,分两种情况:①当![]()
![]() 时,则BN=AM,BM=AC,②当
时,则BN=AM,BM=AC,②当![]()
![]() 时,则BM=AM,BN=AC,分别求出
时,则BM=AM,BN=AC,分别求出![]() 的长,即可.
的长,即可.
∵点![]() 从
从![]() 出发向
出发向![]() 运动,点
运动,点![]() 从
从![]() 出发向
出发向![]() 运动, 速度之比为
运动, 速度之比为![]() ,
,
∴可设点M的速度为2x,点N的速度为3x,运动时间为t,
∴BM=2xt,BN=3xt,AM=20cm-2xt,
①当![]()
![]() 时,则BN=AM,BM=AC,
时,则BN=AM,BM=AC,
∴3xt=20-2xt,得xt=4,
∴AC=BM=2xt=8cm,
②当![]()
![]() 时,则BM=AM,BN=AC,
时,则BM=AM,BN=AC,
∴2xt=20-2xt,得xt=5,
∴AC= BN=3xt=15cm,
故答案是:![]() 或
或![]() .
.
-
科目: 来源: 题型:
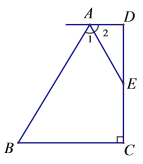
查看答案和解析>>【题目】如图,已知AD∥BC,DC⊥BC, AE平分∠BAD, E为CD中点,试探索AD、BC和AB之间有何关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节临近,某商场决定开展“金秋十月,回馈顾客”的让利活动,对部分品牌月饼进行打折销售,其中甲品牌月饼打八折,乙品牌月饼打七五折.已知打折前,买
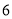 盒甲品牌月饼和
盒甲品牌月饼和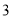 盒乙品牌月饼需
盒乙品牌月饼需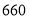 元;打折后,买
元;打折后,买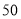 盒甲品牌月饼和
盒甲品牌月饼和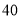 盒乙品牌月饼需
盒乙品牌月饼需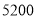 元.
元. (1)打折前甲、乙两种品牌月饼每盒分别为多少元?
(2)幸福敬老院需购买甲品牌月饼
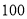 盒,乙品牌月饼
盒,乙品牌月饼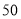 盒,问打折后购买这批月饼比不打折节省了多少钱?
盒,问打折后购买这批月饼比不打折节省了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,发生的概率是
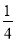 的是( )
的是( )A.从一副扑克牌中,任意抽取其中的一张,抽到红桃的概率
B.一个圆盘被染成红、黄、蓝、紫四种颜色,随机转动一次,转盘停止时,指针刚好指向红色的概率
C.小明开车到十字路口时,遇到红灯的概率
D.一道单选题有
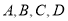 四个备用选项, 从中随机选一个作答,答对的概率
四个备用选项, 从中随机选一个作答,答对的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
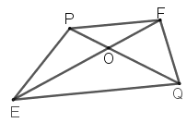
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
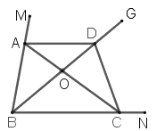
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
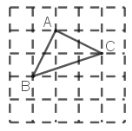
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
-
科目: 来源: 题型:
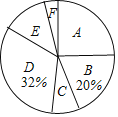
查看答案和解析>>【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分.
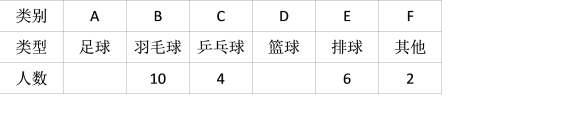
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜欢乒乓球的有 人,最喜欢篮球的学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,其中,最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %;
(3)该校共有450名学生,根据调查结果,估计该校最喜欢排球的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
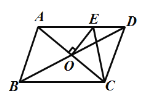
A. 8cm B. 10cm C. 11cm D. 12cm
相关试题

