搜索
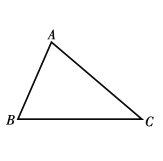
【题目】如图，在
中，
请按要求用尺规作出下列图形(不写作法，但要保留作图痕迹)，并填空．
作出
的平分线交
于点
；
作
交
于点
平行依据是_____ __；
的度数为 ．
参考答案：
【答案】（1）见解析；（2）内错角相等，两直线平行；（3）84°
【解析】
（1）根据角平分线的尺规作图法，即可求解；
（2）根据平行线的判定定理，尺规作∠CDE=∠BCD，即可求解；
（3）根据三角形内角和定理以及角平分线的定义，即可求解．
（1）如图所示：射线
即为所求；
（2）如图所示：直线
即为所求；
由尺规作图得：∠EDC=∠BCD，
∴
，
故答案是：内错角相等，两直线平行；
（3）∵
，
∴∠ACB=180°-62°-74°=44°，
∵CD平分∠ACB，
∴∠BCD=
∠ACB=22°，
∴∠BDC=180°=74°-22°=
．
故答案是：
-
科目： 来源： 题型：
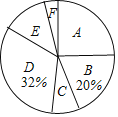
查看答案和解析>>【题目】某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
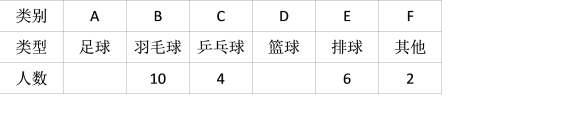
根据以上信息，解答下列问题：
（1）被调查的学生中，最喜欢乒乓球的有 人，最喜欢篮球的学生数占被调查总人数的百分比为 %；
（2）被调查学生的总数为 人，其中，最喜欢篮球的有 人，最喜欢足球的学生数占被调查总人数的百分比为 %；
（3）该校共有450名学生，根据调查结果，估计该校最喜欢排球的学生数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在□ABCD中，O是AC、BD的交点，过点O 与AC垂直的直线交边AD于点E，若□ABCD的周长为22cm，则△CDE的周长为（ ）．
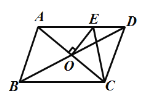
A. 8cm B. 10cm C. 11cm D. 12cm
-
科目： 来源： 题型：
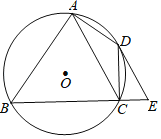
查看答案和解析>>【题目】如图，四边形ABCD内接于⊙O，∠BAD=90°，点E在BC的延长线上，且∠DEC=∠BAC．
（1）求证：DE是⊙O的切线；
（2）若AC∥DE，当AB=8，CE=2时，求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】幻方是一种将数字排在正方形格子中，使每行、每列和每条对角线上的数字和都相等的模型．数学课上，老师在黑板上画出一个幻方如图所示，并设计游戏：一人将一颗能粘在黑板上的磁铁豆随机投入幻方内，另一人猜数，若所猜数字与投出的数字相符，则猜数的人获胜，否则投磁铁豆的人获胜．猜想的方法从以下两种中选一种：
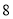
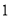
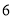
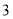
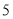
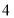
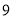
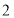
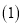猜“是大于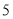的数”或“不是大于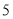的数”；
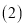猜“是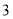的倍数”或“不是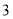的倍数”；如果轮到你猜想，那么为了尽可能获胜，你将选择哪--种猜数方法？怎么猜？为什么？
-
科目： 来源： 题型：
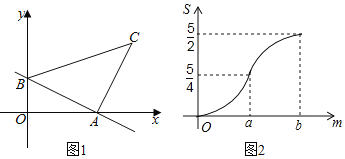
查看答案和解析>>【题目】如图1，直线AB与x轴、y轴分别相交于点A、B，将线段AB绕点A顺时针旋转90°，得到AC，连接BC，将△ABC沿射线BA平移，当点C到达x轴时运动停止．设平移距离为m，平移后的图形在x轴下方部分的面积为S，S关于m的函数图象如图2所示（其中0＜m≤a，a＜m≤b时，函数的解析式不同）．
（1）填空：△ABC的面积为 ；
（2）求直线AB的解析式；
（3）求S关于m的解析式，并写出m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明遇到这样一个问题：
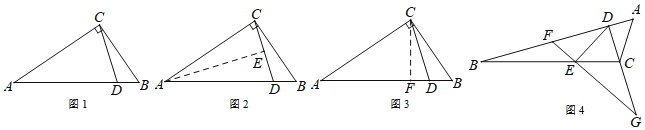
如图1，△ABC中，∠ACB=90°，点D在AB上，且∠BAC=2∠DCB，求证：AC=AD．
小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：
方法1：如图2，作AE平分∠CAB，与CD相交于点E．
方法2：如图3，作∠DCF=∠DCB，与AB相交于点F．
（1）根据阅读材料，任选一种方法，证明AC=AD．
用学过的知识或参考小明的方法，解决下面的问题：
（2）如图4，△ABC中，点D在AB上，点E在BC上，且∠BDE=2∠ABC，点F在BD上，且∠AFE=∠BAC，延长DC、FE，相交于点G，且∠DGF=∠BDE．
①在图中找出与∠DEF相等的角，并加以证明；
②若AB=kDF，猜想线段DE与DB的数量关系，并证明你的猜想．
相关试题
