【题目】如图,△ABC在平面直角坐标系中.
(1)写出△ABC各顶点的坐标.
(2)把△ABC向上平移2个单位,再向右平移2个单位得△A'B'C',在图中画出△A'B'C',并写出A'、B'、C'的坐标.
(3)求出![]() .
.

参考答案:
【答案】(1)A(-1,-1) B(4,2) C(1,3) ;(2) 详见解析,A'(1,1),B'(6,4),C'(3,5);(3)7
【解析】
(1)根据各点所在象限的符号和距坐标轴的距离可得各点的坐标;
(2)根据平移的规律,把△ABC的各顶点向上平移2个单位,再向右平移2个单位,顺次连接各顶点即为△A′B′C′;直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标;
(3)利用△ABC所在的长方形的面积减去四周三个小直角三角形的面积列式计算即可得解.
解:(1)A(-1,-1);B(4,2);C(1,3);
(2)如图,A'(1,1),B'(6,4),C'(3,5).

(3)SΔABC=5×4![]() ×5×3
×5×3![]() ×1×3
×1×3![]() ×2×4
×2×4
=20-7.5-1.5-4
=20-13
=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(一)问题提出:如何把n个边长为1的正方形,剪拼成一个大正方形?
(二)解决方法
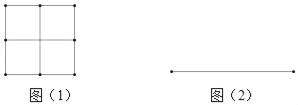
探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积为5,边长为
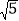 ,可表示成
,可表示成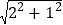 ;
;(2)剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图(3)中的虚线为边,拼成一个边长为
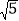 的大正方形,如图(4).
的大正方形,如图(4).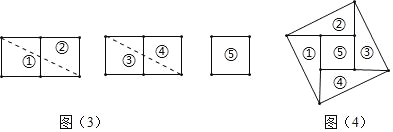
问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
(1)计算:拼成的大正方形的面积为____,边长为_____,可表示成____;
(2)剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
(3)拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队有甲、乙两名射手,他们各自射击7次,射中靶的环数记录如下:
甲:8,8,8,9,6,8,9
乙:10,7,8,8,5,10,8
(1)分别求出甲、乙两名射手打靶环数的平均数、众数、中位数;
(2)如果要选择一名成绩比较稳定的射手,代表射击队参加比赛,应如何选择?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
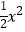 +bx﹣
+bx﹣  的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.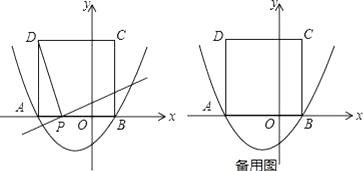
(1)b=;点D的坐标:;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C、D在⊙O上,∠BAC=50°,则∠ADC为( )
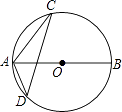
A.40°
B.50°
C.80°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
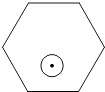
A.πr2
B.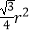
C.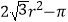 r2
r2
D.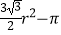 r2
r2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
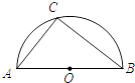
A.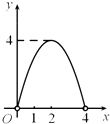
B.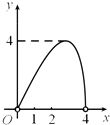
C.
D.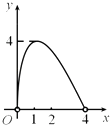
相关试题

