【题目】如图,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,点
上,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 垂直于
垂直于![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
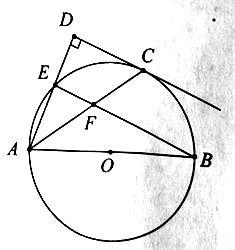
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)16.
【解析】
试题分析:(1)连接OC,由点C是![]() 的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
(2)过点O作OM⊥AC于点M,由点C是![]() 的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=
的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=![]() 可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
试题解析:(1)证明:连接OC,如图1所示.
∵点C是![]() 的中点,∴
的中点,∴![]() ,∴OC⊥BE.
,∴OC⊥BE.
∵AB是⊙O的直径,∴AD⊥BE,∴AD∥OC.
∵AD⊥CD,∴OC⊥CD,
∴CD是⊙O的切线.
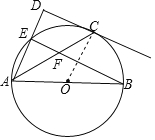
(2)解:过点O作OM⊥AC于点M,如图2所示.
∵点C是![]() 的中点,∴
的中点,∴![]() ,∠BAC=∠CAE,
,∠BAC=∠CAE,
∴![]() .
.
∵cos∠CAD=![]() ,∴
,∴![]() ,∴AB=
,∴AB=![]() BF=20.
BF=20.
在Rt△AOM中,∠AMO=90°,AO=![]() AB=10,cos∠OAM=cos∠CAD=
AB=10,cos∠OAM=cos∠CAD=![]() ,
,
∴AM=AOcos∠OAM=8,∴AC=2AM=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A(4,0),点B是y轴正半轴上一点,如图1,以AB为直角边作等腰直角三角形ABC.

(1)当点B坐标为(0,1)时,求点C的坐标;
(2)如图2,以OB为直角边作等腰直角△OBD , 点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有四张背面完全相同的纸牌
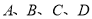 ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.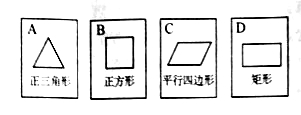
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用
 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=60°,∠B=2∠C,则∠B=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】转基因作物是利用基因工程将原有作物基因加入其它生物的遗传物质,并将不良基因移除,从而造成品质更好的作物.我国现有转基因作物种植面积约为4 200 000公顷,将4 200 000用科学记数法表示为( )
A.4.2×106
B.4.2×105
C.42×105
D.0.42×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,折叠长方形一边AD,使点D落在BC边的点F处,折痕为AE,这时AD = AF,DE = FE.已知BC =5厘米,AB =4厘米.

(1)求BF与FC的长;
(2)求EC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 .
相关试题

