【题目】已知正方形ABCD中,P为直线AD上一点,以PD为边做正方形PDEF,使点E在线段CD的延长线上,连接AC、AF.若![]() ,则
,则![]() 的度数为________.
的度数为________.
参考答案:
【答案】![]() 或
或![]()
【解析】
根据题意需要分三种情况讨论计算:(1)当点P在DA的延长线上时,因为AD<PD,与条件不符,所以这种情况不成立;(2)当点P在线段DA上时,连接FD,根据已知条件和正方形的性质可得△ADF是等腰三角形,顶角是45°,求出底角,从而求解;(3)当点P在AD的延长线上时,连接FD,方法同(2)即可解答.
解:(1)当点P在DA的延长线上时,AD<PD,不符合![]() ,故这种情况不成立;
,故这种情况不成立;
(2)当点P在线段DA上时,如图:
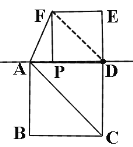
连接FD,∵正方形PDEF中,FD=![]() PD,
PD, ![]() ,∠ADF=45°,
,∠ADF=45°,
∴FD=AD,∠DAF=∠AFD=(180°-45°)÷2=67.5°,
∴![]() =∠CAD+∠DAF=45°+67.5°=
=∠CAD+∠DAF=45°+67.5°=![]() ;
;
(3))当点P在AD的延长线上时,如图:
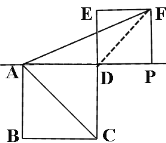
连接FD,∵正方形PDEF中,FD=![]() PD,
PD, ![]() ,∠PDF=45°=∠FAD+∠DFA,
,∠PDF=45°=∠FAD+∠DFA,
∴AD=DF,∠FAD=∠DFA =45°÷2=22.5°,
∴![]() =∠CAD+∠DAF=45°+22.5°=67.5°;
=∠CAD+∠DAF=45°+22.5°=67.5°;
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m)
2.3
2.4
2.5
2.4
2.4
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
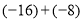
(2)
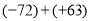
(3)0-(-5)
(4)-2.5-5.9
(5)12-(-18)+(-7)-15
(6)
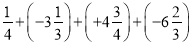
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D.E分别在边AB,AC上,DE∥BC,按下列要求画图并填空
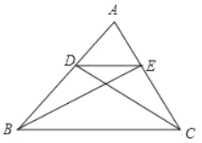
(1)过点E画直线BC的垂线交直线BC于点F;
(2)点D到直线______的距离等于线段EF的长度
(3)联结BE.CD,EBC的面积______DBC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AED=∠C,∠1+∠2=180°.请说明∠BEC=∠FGC
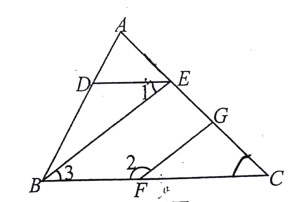
解:因为∠AED=∠C(已知),
所以________∥_______(_________________________________ )
得∠1=∠3( _______________________________ )
又∠1+∠2=180°(已知),
得∠3+∠2=180°(___________________________)
所以_______∥_______
所以∠BEC=∠FGC(___________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.
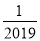 B.2020C.2019D.2018
B.2020C.2019D.2018
相关试题

