搜索
【题目】已知∠AED=∠C,∠1+∠2=180°.请说明∠BEC=∠FGC
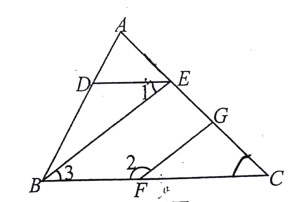
解：因为∠AED=∠C(已知)，
所以________∥_______（_________________________________ ）
得∠1=∠3（ _______________________________ ）
又∠1+∠2=180°（已知），
得∠3+∠2=180°（___________________________）
所以_______∥_______
所以∠BEC=∠FGC（___________________________）
参考答案：
【答案】见解析.
【解析】
首先由∠AED=∠C判定DE∥BC，可得∠1=∠3，再由∠1+∠2=180°，推出∠3+∠2=180°，判定BE∥FG，即可得到∠BEC=∠FGC.
解：因为∠AED=∠C(已知)，
所以DE∥BC（同位角相等，两直线平行）
得∠1=∠3（ 两直线平行，内错角相等 ）
又∠1+∠2=180°（已知），
得∠3+∠2=180°（等量代换）
所以BE∥FG（同旁内角互补，两直线平行）
所以∠BEC=∠FGC（两直线平行，同位角相等）
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）
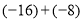
（2）
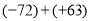
（3）0-（-5）
（4）-2.5-5.9
（5）12-（-18）+（-7）-15
（6）
-
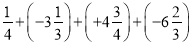
科目： 来源： 题型：
查看答案和解析>>【题目】已知正方形ABCD中，P为直线AD上一点，以PD为边做正方形PDEF，使点E在线段CD的延长线上，连接AC、AF．若
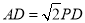，则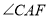
的度数为________. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,点D.E分别在边AB,AC上,DE∥BC,按下列要求画图并填空
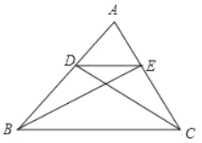
(1)过点E画直线BC的垂线交直线BC于点F;
(2)点D到直线______的距离等于线段EF的长度
(3)联结BE.CD,EBC的面积______DBC的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1＝0（a≠0）有一根为x＝2019，则一元二次方程a（x﹣1）2+b（x﹣1）＝1必有一根为（ ）
A.
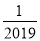B.2020C.2019D.2018 -
科目： 来源： 题型：
查看答案和解析>>【题目】问题情境
小明和小丽共同探究一道数学题：
如图①，在△ABC中，点D是边BC的中点，∠BAD=65°，∠DAC=50°，AD=2，
求AC．
探索发现
小明的思路是：延长AD至点E，使DE=AD，构造全等三角形．
小丽的思路是：过点C作CE∥AB，交AD的延长线于点E，构造全等三角形．
选择小明、小丽其中一人的方法解决问题情境中的问题．
类比应用
如图②，在四边形ABCD中，对角线AC、BD相交于点O，点O是BD的中点，
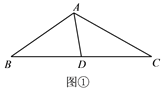
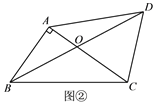
AB⊥AC．若∠CAD=45°，∠ADC=67.5°，AO=2，则BC的长为___________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2﹣2x+c（a≠0）与x轴、y轴分别交于点A，B，C三点，已知点A（﹣2，0），点C（0，﹣8），点D是抛物线的顶点．
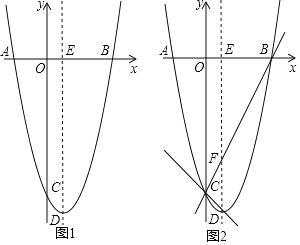
（1）求抛物线的解析式及顶点D的坐标；
（2）如图1，抛物线的对称轴与x轴交于点E，第四象限的抛物线上有一点P，将△EBP沿直线EP折叠，使点B的对应点B'落在抛物线的对称轴上，求点P的坐标；
（3）如图2，设BC交抛物线的对称轴于点F，作直线CD，点M是直线CD上的动点，点N是平面内一点，当以点B，F，M，N为顶点的四边形是菱形时，请直接写出点M的坐标．
相关试题
