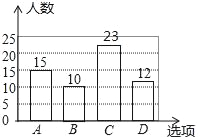
【题目】为了丰富同学的课余生活,某学校将举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是________”的问卷调查,要求学生只能从“A(绿博园),B(人民公园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

回答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)若该学校共有3 600名学生,试估计该校去湿地公园的学生人数.
参考答案:
【答案】(1)60;(2)作图见解析;(3)1380.
【解析】分析:(1)由A的人数及其人数占被调查人数的百分比可得;(2)根据各项目人数之和等于总数可得C选项的人数;(3)用样本中最想去湿地公园的学生人数占被调查人数的比例乘总人数即可.
本题解析:(1)本次调查的样本容量是15÷25%=60;
(2)选择C的人数为:60﹣15﹣10﹣12=23(人),
补全条形图如图:
(3)![]() ×3600=1380(人).
×3600=1380(人).
答:估计该校最想去湿地公园的学生人数约由1380人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内:
0.275,﹣|﹣2|,﹣1.04,﹣(﹣10)2,﹣(﹣8), -
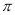 ,0,﹣
,0,﹣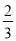 .
.负数集合{ …};
非负整数集合{ …};
整数集合{ …};
分数集合{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,∠MDN的两边分别与AB,AC相交于M,N两点,且∠MDN+∠BAC=180°.
(1)求证AE=AF;
(2)若AD=6,DF=2
 ,求四边形AMDN的面积.
,求四边形AMDN的面积.
-
科目: 来源: 题型:
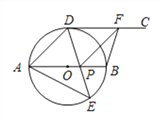
查看答案和解析>>【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=AE,AD与BE相交于点F.
(1)求证:∠ABE=∠CAD;
(2)如图2,以AD为边向左作等边△ADG,连接BG.
ⅰ)试判断四边形AGBE的形状,并说明理由;
ⅱ)若设BD=1,DC=k(0<k<1),求四边形AGBE与△ABC的周长比(用含k的代数式表示).
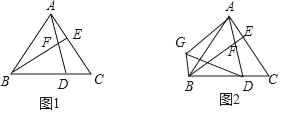
-
科目: 来源: 题型:
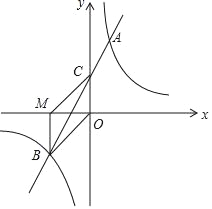
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=
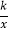 (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2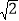 ,点A的纵坐标为4.
,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
参考数据:
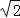 ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
相关试题

