【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 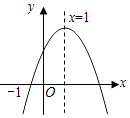
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:①∵抛物线开口向下, ∴a<0.
∵抛物线的对称轴为x=﹣ ![]() =1,
=1,
∴b=﹣2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2﹣4ac>0,④正确.
综上可知:成立的结论有2个.
故选B.
由抛物线的开口方程、抛物线的对称轴以及当x=0时的y值,即可得出a、b、c的正负,进而即可得出①错误;由x=﹣1时,y<0,即可得出a﹣b+c<0,进而即可得出②错误;由抛物线的对称轴为x=1结合x=0时y>0,即可得出当x=2时y>0,进而得出4a+2b+c=c>0,③成立;由二次函数图象与x轴交于不同的两点,结合根的判别式即可得出△=b2﹣4ac>0,④成立.综上即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
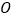 为原点,四边形
为原点,四边形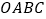 是长方形,点
是长方形,点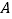 ,
,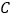 的坐标分别为
的坐标分别为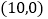 ,
,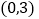 ,
, 是
是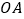 的中点,点
的中点,点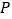 在边
在边 上运动,当
上运动,当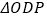 是腰长为5的等腰三角形时,点
是腰长为5的等腰三角形时,点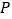 的坐标为_______.
的坐标为_______.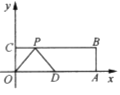
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
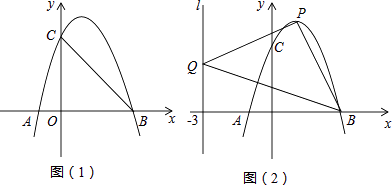
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 ,
, 的坐标分别为
的坐标分别为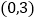 ,
,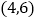 ,点
,点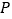 是
是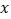 轴上的一个动点,若点
轴上的一个动点,若点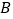 关于直线
关于直线 的对称点
的对称点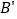 恰好落在坐标轴上,则点
恰好落在坐标轴上,则点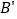 的坐标为_______.
的坐标为_______. 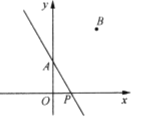
-
科目: 来源: 题型:
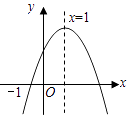
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象的一部分,则一元二次方程的两根分别为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
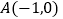 ,
,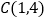 ,点
,点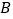 在
在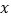 轴上,且
轴上,且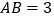 .
.(1)求点
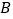 的坐标,并画出
的坐标,并画出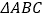 ;
;(2)求
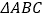 的面积;
的面积;(3)在
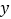 轴上是否存在点
轴上是否存在点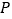 ,使以
,使以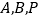 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕着点C顺时针方向旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是 .

相关试题

