【题目】已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
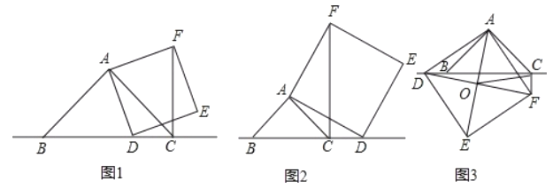
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF. ②![]() .
.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系,
②若连接正方形对角线AE,DF,交点为0,连接OC,探究△AOC的形状,并说明理由.
参考答案:
【答案】(1)①见解析;②见解析;(2)见解析(3)①见解析;②见解析.
【解析】
(1)①根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,再根据正方形的性质可得AD=AF,∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠ACF+∠ACB=90°,从而得证;②根据全等三角形对应边相等可得BD=CF,从而求出CF=BC-CD;
(2)与(1)同理可得BD=CF,然后结合图形可得CF=BC+CD;
(3)①与(1)同理可得BD=CF,然后结合图形可得CF=CD-BC;②根据等腰直角三角形的性质求出∠ABC=∠ACB=45°,再根据邻补角的定义求出∠ABD=135°,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,根据全等三角形对应角相等可得∠ACF=∠ABD,再求出∠FCD=90°,然后根据直角三角形斜边上的中线等于斜边的一半求出OC=![]() DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.
(1)证明:①∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中, 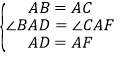
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BD⊥CF;
②由①△BAD≌△CAF可得BD=CF,
∵BD=BC-CD,
∴CF=BC-CD;
(2)与(1)同理可得BD=CF,
所以,CF=BC+CD;
(3)①与(1)同理可得,BD=CF,
所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAF+∠CAF=90°,
∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,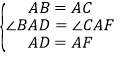
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°,
∴∠FCD=∠ACF-∠ACB=90°,
则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点,
∴OC=![]() DF,
DF,
∵在正方形ADEF中,OA=![]() AE,AE=DF,
AE,AE=DF,
∴OC=OA,
∴△AOC是等腰三角形.
-
科目: 来源: 题型:
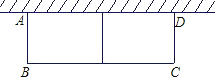
查看答案和解析>>【题目】如图所示,某农户想建造一花圃,用来种植两种不同的花卉,以供应城镇市场需要,现用长为36m的篱笆,一面砌墙(墙的最大可使用长度l=13m),围成中间隔有一道篱笆的长方形花圃,设花圃宽AB为x,面积为S.
(1)求S与x的函数关系式.并指出它是一次函数,还是二次函数?
(2)若要围成面积为96m2的花圃,求宽AB的长度.
(3)花圃的面积能达到108m2吗?若能,请求出AB的长度,若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
探究发现:如图所示,小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为(a+b)的正方形(其中a、b的和不变,但a、b的数值及两者的大小关系都可以变化).仔细观察拼图,我们发现,如果右图中间有空白图形F,那么它一定是正方形
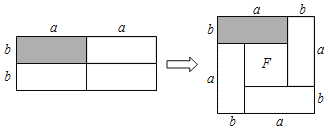
(1)空白图形F的边长为 ;
(2)通过计算左右两个图形的面积,我们发现(a+b)2、(a﹣b)2和ab之间存在一个等量关系式.
①这个关系式是 ;
②已知数x、y满足:x+y=6,xy=
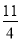 ,则x﹣y= ;
,则x﹣y= ;问题解决:
问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
①对于周长一定的长方形,设周长是20,则长a和宽b的和是 面积S=ab的最大值为 ,此时a、b的关系是 ;
②对于周长为L的长方形,面积的最大值为 .
活动经验:
周长一定的长方形,当邻边长度a、b满足 时面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校组织中国共产党第十九次全国代表大会知识问答,共设有20道选择题,各题分值相同,每题必答.下表记录了A、B、D三名参赛学生的得分情况:
参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
94
D
14
6
64
则参赛学生E的得 分可能 是( )
A.93B.87C.66D.40
-
科目: 来源: 题型:
查看答案和解析>>【题目】梦洁和嘉丽是邻居,星期天他们两家人准备去郊外的农家乐游玩,早上两家人同时乘坐了两辆不同价格的出租车,梦洁家乘坐的是起步4公里8元,以后每公里收1.2元,嘉丽家乘坐的是起步3公里6元,以后每公里收1.3元,两家人几乎同时到达农家乐,付款后梦洁发现两家人的车费仅差1.5元,则两家住地离公园的路程是( )
A.
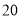 公里B.
公里B.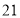 公里C.
公里C. 公里D.
公里D.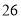 公里
公里 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90,AB=BC=
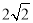 ,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )
,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )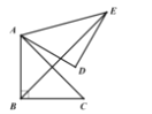
A. 2+
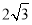 B. 2
B. 2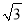 C. 2+2
C. 2+2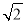 D. 2
D. 2 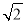
-
科目: 来源: 题型:
查看答案和解析>>【题目】运算律是解决许多数学问题的基础,在运算中有重要的作用,充分运用运算律能使计算简便高效.
例如:(-125
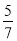 )÷(-5)
)÷(-5)解:(-125
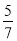 )÷(-5)=125
)÷(-5)=125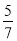 ×
×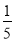 =(125+
=(125+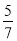 )×
)×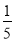 =125×
=125×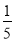 +
+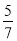 ×
×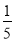 =25+
=25+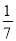 =25
=25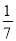
(1)计算:6÷(-
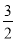 +
+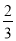 ),A同学的计算过程如下:
),A同学的计算过程如下:原式=6×(-
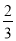 )+6×
)+6×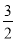 =-6+9=3.
=-6+9=3.请你判断A同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考例题,用运算律简便计算(请写出具体的解题过程):
999×118
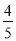 +333×(-
+333×(-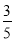 )-999×18
)-999×18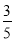 .
.
相关试题

