【题目】如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.
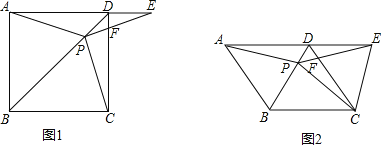
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
参考答案:
【答案】(1)见解析;(2)△PCE是等边三角形.理由见解析.
【解析】
(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=EDF=90°,推出△PEC是等腰直角三角形;
(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA═PE=PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.
(1)证明:如图1中,
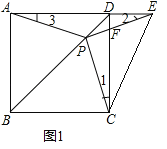
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,
在△PDA和△PDC中,
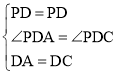 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,
∴∠1=∠2,
∵∠EDF=90°,∠DFE=∠PFC,
∴∠FPC=EDF=90°,
∴△PEC是等腰直角三角形.
(2)解:如图2中,结论:△PCE是等边三角形.
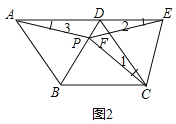
理由:∵四边形ABCD是菱形,
∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,
在△PDA和△PDC中,
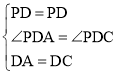 ,
,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,PA═PE=PC,
∴∠1=∠2,
∵∠DFE=∠PFC,
∴∠EPC=∠EDC,
∵∠ADC=120°,
∴∠EDC=60°,
∴∠EPC=60°,
∵PE=PC,
∴△PEC是等边三角形.
-
科目: 来源: 题型:
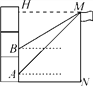
查看答案和解析>>【题目】如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1 m.
(1)AB=________m;
(2)求旗杆MN的高度.(结果保留两位小数)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
-
科目: 来源: 题型:
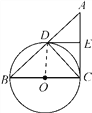
查看答案和解析>>【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
(1)求证:DE是⊙O的切线;
(2)若BD=4,CD=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年是中国工农红军长征胜利80周年,某商家用1200元购进了一批长征胜利主题纪念衫,上市后果然供不应求,商家又用2800元购进了第二批这种纪念衫,所购数量是第一批购进量的2倍,但单价贵了5元.
(1)该商家购进的第一批纪念衫单价是多少元?
(2)若两批纪念衫按相同的标价销售,最后剩下20件按标价八折优惠卖出,如果两批纪念衫全部售完利润不低于640元(不考虑其它因素),那么每件纪念衫的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师给出了如下问题:

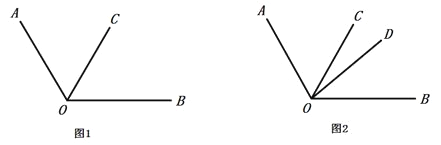
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为
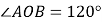 ,
,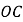 平分
平分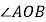 ,
,所以
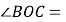 ______
______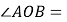 ______
______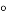 (角平分线的定义).
(角平分线的定义).因为
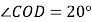 ,
,所以
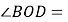 ______
______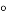 .
.(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是
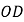 在
在 内部的情况,事实上,
内部的情况,事实上,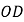 还可能在
还可能在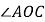 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出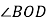 的度数:______.
的度数:______. -
科目: 来源: 题型:
查看答案和解析>>【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段
 ,点
,点 在线段
在线段 上,当点
上,当点 是线段
是线段 和线段
和线段 的中点时,线段
的中点时,线段 的长为_________;若点
的长为_________;若点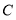 在线段
在线段 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段 与线段
与线段 之间的数量关系为_________.
之间的数量关系为_________. 
(2)应用:
如图3,现有长为40米的拔河比赛专用绳
 ,其左右两端各有一段(
,其左右两端各有一段( 和
和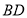 )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳 . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳 ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:①在图中标出点
 、点
、点 的位置,并简述画图方法;
的位置,并简述画图方法;②请说明①题中所标示
 点的理由.
点的理由. 
相关试题

