【题目】数学课上,老师给出了如下问题:

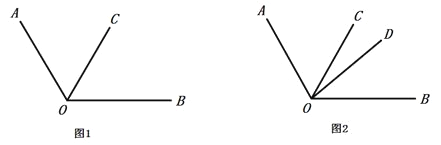
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为![]() ,
,![]() 平分
平分![]() ,
,
所以![]() ______
______![]() ______
______![]() (角平分线的定义).
(角平分线的定义).
因为![]() ,
,
所以![]() ______
______![]() .
.
(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是![]() 在
在![]() 内部的情况,事实上,
内部的情况,事实上,![]() 还可能在
还可能在![]() 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出![]() 的度数:______.
的度数:______.
参考答案:
【答案】(1)![]() ;60°;40° (2)80°
;60°;40° (2)80°
【解析】
(1)依据角平分线的定义,即可得到∠BOC=![]() ∠AOB=60°,再根据角的和差关系,即可得出∠BOD的度数.
∠AOB=60°,再根据角的和差关系,即可得出∠BOD的度数.
(2)依据角平分线的定义,即可得到∠BOC=![]() ∠AOB=60°,再根据角的和差关系,即可得出∠BOD的度数.
∠AOB=60°,再根据角的和差关系,即可得出∠BOD的度数.
(1)如图2,∵∠AOB=120°,OC平分∠AOB.
∴∠BOC=![]() ∠AOB=60°.
∠AOB=60°.
∵∠COD=20°,
∴∠BOD=60°-20°=40°.
故答案为:![]() ;60°;40°;
;60°;40°;
(2)如图1,
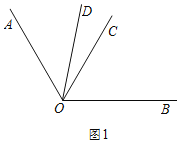
∵∠AOB=120°,OC平分∠AOB.
∴∠BOC=![]() ∠AOB=60°.
∠AOB=60°.
∵∠COD=20°,
∴∠BOD=60°+20°=80°.
故答案为:80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定一个十进制下的自然数
 ,对于
,对于 每个数位上的数,求出它除以
每个数位上的数,求出它除以 的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数
的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数 的“模二数”,记为
的“模二数”,记为 .如
.如 .对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定:
.对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定: 与
与 相加得
相加得 ;
; 与
与 相加得
相加得 与
与 相加得
相加得 ,并向左边一位进
,并向左边一位进 .如
.如 的“模二数”
的“模二数” 相加的运算过程如下图所示.
相加的运算过程如下图所示.
根据以上材料,解决下列问题:
(1)
 的值为______ ,
的值为______ ,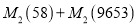 的值为_
的值为_ (2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.如
 ,因为
,因为 ,所以
,所以 ,即
,即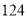 与
与 满足“模二相加不变”.
满足“模二相加不变”.①判断
 这三个数中哪些与
这三个数中哪些与 “模二相加不变”,并说明理由;
“模二相加不变”,并说明理由;②与
 “模二相加不变”的两位数有______个
“模二相加不变”的两位数有______个 -
科目: 来源: 题型:
查看答案和解析>>【题目】济南市地铁1号线,北起方特站,南至工研院站,共设11个车站,2019年4月1日正式开通运营,标志着济南市正式迈进“地铁时代”.11个站点如图所示:

某天,王红从玉符河站开始乘坐地铁,在地铁各站点做志配者服务,到A站下车时,本次志照者服务活动结束,约定向工研院站方向为正,当天的乘车记录如下(单位;站):+3、-2、-6、+7、-5、+3、+6.
(1)请通过计算说明A站是哪一站?
(2)若相邻两站之间的距离为3千米,求这次王红志照服务期间乘坐地铁行进的路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园内要铺设一段长方形步道,须用一些型号相同的灰色正方形地砖和一些型号相同 的白色等腰直角三角形地砖按如图所示方式排列.

(1) 若排列正方形地砖40块,则需使用三角形地砖____________块;
(2) 若排列三角形地砖2 020块,则需使用正方形地砖____________块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
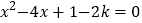 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数
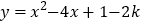 与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标. -
科目: 来源: 题型:
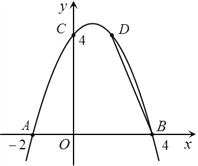
查看答案和解析>>【题目】如图, 已知抛物线
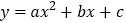 经过A(-2,0)、B(4,0)、C(0,4)三点.
经过A(-2,0)、B(4,0)、C(0,4)三点.(1)求此抛物线的解析式;
(2)此抛物线有最大值还是最小值?请求出其最大或最小值;
(3)若点D(2,m)在此抛物线上,在y轴的正半轴上是否存在点P,使得△BDP是等腰三角形?若存在,请求出所有符合条件的P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学单元测试,七年级第一小组共10名同学,小组长把超过班级平均分的部分记为“+”,不足的部分记为“-”,记录如表:
与平均分的差值(分)
-15
-9
0
+3
+12
+17
人数
1
2
1
2
3
1
根据表格数据解答下列问题:
(1)第一小组同学的平均分比班级平均分高还是低?高或低多少分?
(2)若该班这次测试的平均分为80分,求第一小组10名同学的总分.
相关试题

