【题目】已知,直线l1:y=3x﹣2k与直线l2:y=x+k交点P的纵坐标为5,直线l1与直线l2与y轴分别交于A、B两点.
(1)求出点P的横坐标及k的值;
(2)求△PAB的面积;
(3)点M为直线l1上的一个动点,当△MAB面积与△PAB面积之比为2:3时,求此时的点M的坐标【1】

参考答案:
【答案】(1)P的横坐标为3,k的值是2;(2)9;(3)(2,2)或(﹣2,﹣6).
【解析】
(1)把y=5代入两个函数的解析式,联立即可求出点P的横坐标及k的值;
(2)根据(1)中的结果可以分别求得两条直线的解析式,从而可以求得点A和点B的坐标,进而求得△PAB的面积;
(3)根据(2)中的结果和题意可以求得△MAB的面积,进而求得点M的坐标.
解:(1)∵直线l1:y=3x﹣2k与直线l2:y=x+k交点P的纵坐标为5,
∴5=2x﹣2k,得x=![]() ,5=x+k,得x=5﹣k,
,5=x+k,得x=5﹣k,
∴![]() =5﹣k,
=5﹣k,
解得,k=2,
∴x=3,
即点P的横坐标为3,k的值是2;
(2)∵k=2,
∴直线l1:y=3x﹣4与直线l2:y=x+2,
∵直线l1与直线l2与y轴分别交于A、B两点,
∴点A(0,﹣4),点B(0,2),
又∵点P(3,5),
∴△PAB的面积是![]() =9;
=9;
(3)∵点M为直线l1上的一个动点,△MAB面积与△PAB面积之比为2:3,△PAB的面积是9,
∴△MAB的面积是9÷3×2=6,
设点M的坐标为(m,n),
则![]() =6,
=6,
解得,m=±2,
∵直线l1:y=3x﹣4,点M在直线l1上,
∴当m=2时,n=2,当m=﹣2时,n=﹣6,
故答案为:(2,2)或(﹣2,﹣6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)用不同的方法计算如图中阴影部分的面积得到的等式: ;
(2)如图是两个边长分别为
 、
、 、
、 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是 的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;(3)根据上面两个结论,解决下面问题:若如图中,直角
 三边a、
三边a、 、c,
、c,①满足
 ,ab=18,求
,ab=18,求 的值;
的值;②在①的条件下,若点
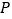 是边
是边 上的动点,连接
上的动点,连接 ,求线段
,求线段 的最小值;
的最小值;③若
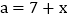 ,
, ,且
,且 ,则
,则 的值是 .
的值是 . 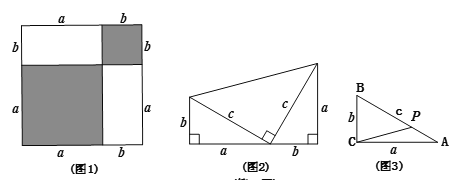
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的游艺会上,投飞标游艺区游戏区规则如下,如图投到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点)现统计小华、小明和小芳掷中与得分情况如图所示.

(1)求掷中A区、B区一次各得多少分?
(2)依此方法计算小明的得分为多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=
 ∠ABC,∠PCD=
∠ABC,∠PCD= ∠ACD,
∠ACD,试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,tanA=1,那么cosB等于( )
A.
B.
C.1
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣2|+( )﹣1﹣(
)﹣1﹣(  ﹣2010)0﹣
﹣2010)0﹣  tan60°
tan60°
(2)先化简,再求值: ÷(x﹣
÷(x﹣  ),其中x=
),其中x=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
相关试题

