【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
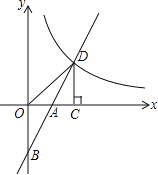
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
参考答案:
【答案】解:(1)当b=﹣2时,直线y=2x﹣2与坐标轴交点的坐标为A(1,0),B(0,﹣2),
∵△AOB≌△ACD,∴CD=DB=2,AO=AC=1。∴点D的坐标为(2,2)。
∵点D在双曲线![]() ( x>0)的图象上,∴k=2×2=4。
( x>0)的图象上,∴k=2×2=4。
(2)直线y=2x+b与坐标轴交点的坐标为A(![]() ,0),B(0,b),
,0),B(0,b),
∵△AOB≌△ACD,∴CD=OB= b,AO=AC=![]() ,
,
∴点D的坐标为(﹣b,﹣b)。
∵点D在双曲线![]() ( x>0)的图象上,
( x>0)的图象上,
∴![]() ,即k与b的数量关系为:
,即k与b的数量关系为:![]() 。
。
直线OD的解析式为:y=x。
【解析】
试题(1)首先求出直线y=2x﹣2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,由点D在双曲线![]() ( x>0)的图象上求出k的值。
( x>0)的图象上求出k的值。
(2)首先直线y=2x+b与坐标轴交点的坐标为A(![]() ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式。
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式。
-
科目: 来源: 题型:
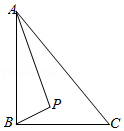
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A.
B.2
C.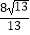
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出
 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:
 填表:
填表:平均数(分)
中位数(分)
众数(分)
初中代表队


高中代表队


 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好; 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定. -
科目: 来源: 题型:
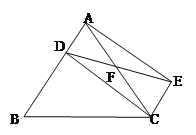
查看答案和解析>>【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=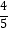 ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中有四点A(﹣2,0),B(﹣1,0),C(0,1),D(0,2)在A、B、C、D中取两点与点O为顶点作三角形,所作三角形是等腰直角三角形的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC中,当顶角A的大小确定时,它的对边BC与邻边(腰AB或AC)的比值确定,记为f(A),易得f(60°)=1.若α是等腰三角形的顶角,则f(α)的取值范围是 .
相关试题

