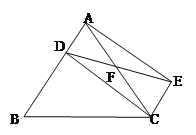
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
参考答案:
【答案】(1)见解析 (2)![]()
【解析】(1)首先利用ASA得出△DAF≌△ECF,进而利用全等三角形的性质得出CE=AD,即可得出四边形ACDE是平行四边形;
(2)由AE⊥EC,四边形ADCE是平行四边形,可推出四边形ADCE是矩形,由F为AC的中点,求出AC,根据勾股定理即可求得AE,由矩形面积公式即可求得结论.
(1) ∵CE∥AB,
∴∠EDA=∠DEC.
∵FA=FC ∠DFA=∠CFE,
∴△ADF≌△CEF(ASA) ,
∴AF=CF,
∴四边形ADCE是平行四边形;
(2)∵AE⊥EC,
综合(1)四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
∴DE=2EF=2 ∠DCE=![]() ,
,
∴DC=![]() ,
,
四边形ADCE的面积=CE·DC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是等腰△ABC底边BC上的高,sinB=
 ,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
,点E在AC上,且AE:EC=2:3,则tan∠ADE=( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
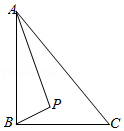
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A.
B.2
C.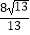
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出
 名选手组成初中代表队和高中代表队参加学校决赛.每个队
名选手组成初中代表队和高中代表队参加学校决赛.每个队 名选手的决赛成绩如图所示:
名选手的决赛成绩如图所示:
 填表:
填表:平均数(分)
中位数(分)
众数(分)
初中代表队


高中代表队


 结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好; 计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线
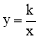 (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.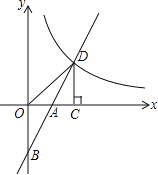
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=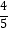 ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中有四点A(﹣2,0),B(﹣1,0),C(0,1),D(0,2)在A、B、C、D中取两点与点O为顶点作三角形,所作三角形是等腰直角三角形的概率是 .
相关试题

