【题目】(1)问题发现
如图1,四边形ABCD为矩形,AB=a,BC=b,点P在矩形ABCD的对角线AC上,Rt△PEF的两条直角边PE,PF分别交BC,DC于点M,N,当PM⊥BC,PN⊥CD时,![]() = (用含a,b的代数式表示).
= (用含a,b的代数式表示).
(2)拓展探究
在(1)中,固定点P,使△PEF绕点P旋转,如图2,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
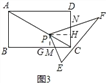
如图3,四边形ABCD为正方形,AB=BC=a,点P在对角线AC上,M,N分别在BC,CD上,PM⊥PN,当AP=nPC时,(n是正实数),直接写出四边形PMCN的面积是 (用含n,a的代数式表示)

参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3) ![]()
【解析】分析:(1)先判断出△PMC∽△ABC,得出![]() ,再判断出四边形CNPM是矩形,即可得出结论;
,再判断出四边形CNPM是矩形,即可得出结论;
(2)先过P作PG⊥BC于G,作PH⊥CD于H,判定△PGM∽△PHN,再根据相似三角形的性质以及平行线分线段成比例定理进行推导计算即可;
(3)先判定△PMC∽△ABC,再根据相似三角形的对应边成比例进行求解,再计算其面积;
详解:
(1)∵四边形ABCD是矩形,
∴AB⊥BC,
∵PM⊥BC,
∴△PMC∽△ABC
∴![]()
∵四边形ABCD是矩形,
∴∠BCD=90°,
∵PM⊥BC,PN⊥CD,
∴∠PMC=∠PNC=90°=∠BCD,
∴四边形CNPM是矩形,
∴CM=PN,
∴![]() ,
,
故答案为![]() ;
;
(2)如图3,过P作PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°
∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴![]()
由PG∥AB,PH∥AD可得,![]() ,
,
∵AB=a,BC=b
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
故答案为![]() ;
;
(3)∵PM⊥BC,AB⊥BC
∴△PMC∽△ABC
∴![]()
当AP=nPC时(n是正实数),![]()
∴PM=![]() a
a
∴四边形PMCN的面积=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),一平面直角坐标第xOy中,直线
 与y轴相交于点A,与反比例函数
与y轴相交于点A,与反比例函数 (x>0)的图像相交于点B(m,2)
(x>0)的图像相交于点B(m,2)(1)求反比例函数的表达式;
(2)若将直线
 向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;
向上平移4个单位长度后与y轴交于点C,求ΔABC的面积;(3)如图(2)将直线
 向上平移,与反比例函数的图像交于点D,连接DA,DB.若
向上平移,与反比例函数的图像交于点D,连接DA,DB.若ΔABC的面积为3,求平移后直线的表达式。


图(1) 图(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学图书馆上周借书记录如下(以100册为标准,超过的册数记为正,不足的册数记为负):

(1)上星期五借出多少册?
(2)上星期四比上星期三多借出多少册?
(3)上周平均每天借出多少册?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列各式:
 =
= ,
, =
= ,
, =
=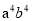 …回答下列三个问题:
…回答下列三个问题:(1)验证:
 =_______,
=_______, ×
× =_______;
=_______;(2)通过上述验证,归纳得出:
 =_______;
=_______;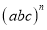 =_______.
=_______.(3)请应用上述性质计算:
 ×
× ×
× .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元时,每天可售出40件,若每件降价10元,则第天多售出10件,请根据以上信息解答下列问题:
(1)为了使销售该品牌衬衫每天获利4500元,并且让利于顾客,每件售价应为多少元;
(2)该服装店将该品牌的衬衫销售完,在补货时厂家只剩100件,经协商每件降价a元,全部拿回。按(1)中的价格售出80件后,剩余的按八折销售。售完这100件衬衫获利20%,求a的值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

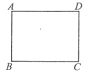
图(1) 图(2) 图(3)
操作探究
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和
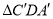 两张纸片
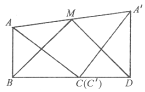
两张纸片(2)将两张纸片如图(2)摆放,点C和
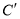 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接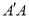 ,记
,记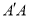 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
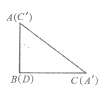
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:(3)如图(3),将两张纸片叠合在一起,然后将
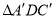 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接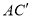 和
和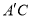 ,探究并直接写出线段
,探究并直接写出线段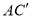 与
与 的关系。
的关系。 -
科目: 来源: 题型:
查看答案和解析>>【题目】莹莹家里今年种植的猕猴桃获得大丰收,星期六从外地来了一位客商到村子里收购猕猴桃.莹莹家卖给了该客商10箱猕猴桃.莹莹在家里帮助爸爸记账,每标准箱猕猴桃的净重为5千克,超过标准数的部分记为“+”,不足标准数的部分记为“﹣”,莹莹的记录如下:+0.4、+0.6、﹣0.2、+0.1、﹣0.6、﹣0.3、+0.4、0、+0.7、﹣0.3.
(1)请计算这10箱猕猴桃的总重为多少千克?
(2)如果弥猴桃的价格为9元/千克,莹莹家出售这10箱猕猴桃共收入多少元?(精确到1元)
(3)若都用这种纸箱装,莹莹家的猕猴桃共能装约2000箱,按照目前这个价格,把猕猴桃全部出售,莹莹家大约能收入多少元?(精确到万位)
相关试题

