搜索
【题目】某服装店专营一批进价为每件200元的品牌衬衫，每件售价为300元时，每天可售出40件，若每件降价10元，则第天多售出10件，请根据以上信息解答下列问题：
（1）为了使销售该品牌衬衫每天获利4500元，并且让利于顾客，每件售价应为多少元；
（2）该服装店将该品牌的衬衫销售完，在补货时厂家只剩100件，经协商每件降价a元，全部拿回。按（1）中的价格售出80件后，剩余的按八折销售。售完这100件衬衫获利20%，求a的值。
参考答案：
【答案】（1）该品牌衬衫每件售价应为250元；（2）a的值是40
【解析】试题分析：（1）表示出每件商品的利润和销量进而得出等式求出答案；
（2）分别表示出100件商品的利润进而得出等式求出答案．
试题解析：
（1）设该品牌衬衫每件售价应为x元，根据题意，得
解，得
因为要让利于顾客，所以应采用降价销售且降得越多越好，
∴x=250.
答：该品牌衬衫每件售价应为250元.
(2)方法一：根据题意，得
解，得a=40
答：a的值是40
方法二：根据题意：得
解，得a=40
经检验a=40是原方程的解。
答：a的值是40
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学图书馆上周借书记录如下（以100册为标准，超过的册数记为正，不足的册数记为负）：
（1）上星期五借出多少册？
（2）上星期四比上星期三多借出多少册？
（3）上周平均每天借出多少册？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列各式：
=
，
=
，
=
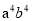…回答下列三个问题：（1）验证：
=_______，
×
=_______；（2）通过上述验证，归纳得出：
=_______；
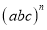=_______．（3）请应用上述性质计算：
×
×
． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现
如图1，四边形ABCD为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF的两条直角边PE，PF分别交BC，DC于点M，N，当PM⊥BC，PN⊥CD时，
= （用含a，b的代数式表示）．（2）拓展探究
在（1）中，固定点P，使△PEF绕点P旋转，如图2，
的大小有无变化？请仅就图2的情形给出证明．（3）问题解决
如图3，四边形ABCD为正方形，AB=BC=a，点P在对角线AC上，M，N分别在BC，CD上，PM⊥PN，当AP=nPC时，（n是正实数），直接写出四边形PMCN的面积是 （用含n，a的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践
问题情境
如图，同学们用矩形纸片ABCD开展数学探究活动，其中AD=8，CD=6。
操作计算
（1）如图（1），分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片，如果剩余的纸片BEDF菱形，求AE的长；
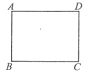
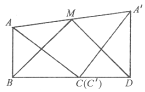
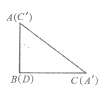
图（1） 图（2） 图（3）
操作探究
把矩形纸片ABCD沿对角线AC剪开，得到ΔABC和
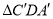两张纸片(2)将两张纸片如图（2）摆放，点C和
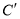重合，点B,C,D在同一条直线上，连接
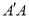,记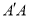
的中点为M，连接BM，MD，发现ΔBMD是等腰三角形，请证明：（3）如图（3），将两张纸片叠合在一起，然后将
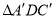纸片绕点B顺时针旋转a（00<a<900),连接
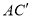和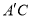
，探究并直接写出线段
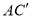与
的关系。 -
科目： 来源： 题型：
查看答案和解析>>【题目】莹莹家里今年种植的猕猴桃获得大丰收，星期六从外地来了一位客商到村子里收购猕猴桃．莹莹家卖给了该客商10箱猕猴桃．莹莹在家里帮助爸爸记账，每标准箱猕猴桃的净重为5千克，超过标准数的部分记为“+”，不足标准数的部分记为“﹣”，莹莹的记录如下：+0.4、+0.6、﹣0.2、+0.1、﹣0.6、﹣0.3、+0.4、0、+0.7、﹣0.3．
（1）请计算这10箱猕猴桃的总重为多少千克？
（2）如果弥猴桃的价格为9元/千克，莹莹家出售这10箱猕猴桃共收入多少元？（精确到1元）
（3）若都用这种纸箱装，莹莹家的猕猴桃共能装约2000箱，按照目前这个价格，把猕猴桃全部出售，莹莹家大约能收入多少元？（精确到万位）
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（ ）
A.750平方千米B.75平方千米C.15平方千米D.7.5平方千米
相关试题
