【题目】如图,已知AB∥CD,点P在直线BD上(点P与点B、D不重合),分别记∠BAP,∠DCP,∠APC为∠1,∠2,∠3.
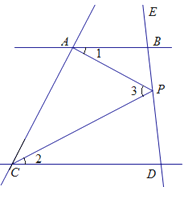
(1)当点P在B、D两点间移动时,写出∠1,∠2,∠3之间的等量关系,并说明理由;
(2)当点P在射线BE上移动时,(1)中的等量关系还存在吗?若存在,请说明理由;若不存在,请写出一个你认为正确的等量关系,并说明理由。
参考答案:
【答案】(1)等量关系:∠3=∠1+∠2,(2)(1)中等量关系不存在了.
【解析】(1)首先过点P作PQ∥AB,由于AB∥CD,可得PQ∥CD,然后由两直线平行,同位角相等,求得答案;(2)由题意画出图形得知,(1)中的等量关系不存在了.
解:(1)等量关系:∠3=∠1+∠2,
作PQ∥AB,
∵AB∥CD,∴PQ∥CD,
∴∠APQ=∠1,∠CPQ=∠2,
∴∠3=∠APQ +∠CPQ=∠1+∠2
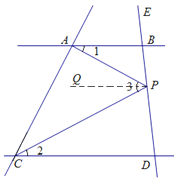
(2)答:(1)中等量关系不存在了.
如图所示

AB∥CD
∴ ∠1= ∠PCD
∴∠2+∠1=180°
∠2+∠APC+∠PAB=180°
∴∠PCD=∠1=∠APC+∠PAB
“点睛”本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.合理添加平行线是解决此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏和小聪进行百米赛跑,小敏每秒跑6.3米,小聪每秒跑7.1米,小聪让小敏先跑5米,则比赛结果是( )
A.小敏和小聪同时到达终点
B.小敏比小聪早近1秒到达终点
C.小敏比小聪晩近1秒到达终点
D.小敏比小聪晩近0.9秒到达终点 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=(m﹣1)x2m2﹣3是反比例函数,则m的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次身体的体检中,小红、小强、小林三人的平均体重为42kg,小红、小强的平均体重比小林的体重多6kg,小林的体重是___kg.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,BE=DF.
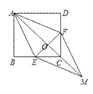
(1)求证:AE=AF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.

(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
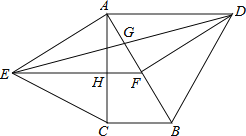
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
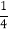 BD
BD其中正确结论的为______(请将所有正确的序号都填上).
相关试题

