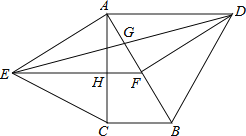
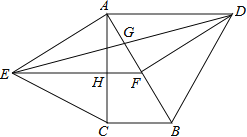
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
参考答案:
【答案】①③④
【解析】试题分析:根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形而不是菱形,根据平行四边形的性质得出AD=4AG,从而得到答案.
解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF=![]() BC,
BC,
∵BC=![]() AB,AB=BD,
AB,AB=BD,
∴HF=![]() BD,故④说法正确;
BD,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG=![]() AF,
AF,
∴AG=![]() AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故答案为:①③④.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,点P在直线BD上(点P与点B、D不重合),分别记∠BAP,∠DCP,∠APC为∠1,∠2,∠3.
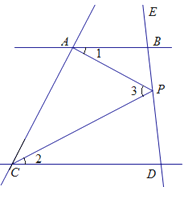
(1)当点P在B、D两点间移动时,写出∠1,∠2,∠3之间的等量关系,并说明理由;
(2)当点P在射线BE上移动时,(1)中的等量关系还存在吗?若存在,请说明理由;若不存在,请写出一个你认为正确的等量关系,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,BE=DF.
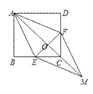
(1)求证:AE=AF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.

(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,则点A在⊙C____________,点B在⊙C____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】到定点O的距离等于4的点的集合是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)按照以上变换,那么f(g(a,b))等于( )
A. (﹣b,﹣a) B. (a,b) C. (b,a) D. (﹣a,﹣b)
相关试题

