【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形. 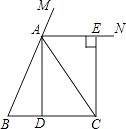
参考答案:
【答案】证明:∵AN是△ABC外角∠CAM的平分线, ∴∠MAE= ![]() ∠MAC,
∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∵CE⊥AN,
∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形).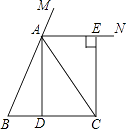
【解析】根据AN是△ABC外角∠CAM的平分线,推得∠MAE= ![]() (∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).

(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′ , 并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为
 ,点B表示的数为
,点B表示的数为 .
.(1)若A、B移动到如图所示位置,计算
 的值.
的值.(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数
 ,并计算
,并计算 .
.(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时
 比
比 大多少?请列式计算.
大多少?请列式计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学文化课题活动中,把一副数学文化创意扑克牌中的4张扑克牌(如图所示)洗匀后正面向下放在桌面上,从中随机抽取2张牌,请你用列表或画树状图的方法,求抽取的2张牌的数字之和为偶数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.

(1)求AD的长;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB=
 BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明.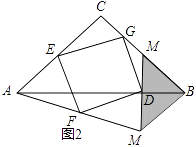
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球。
某校羽毛球队需要购买
 副球拍和
副球拍和 盒羽毛球
盒羽毛球 .
.(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含
 、
、 的代数式表示;
的代数式表示;(2)当
 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?(3)当
 、
、 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
相关试题

