【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
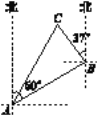
参考答案:
【答案】救援船的航行速度大约是64海里/时.
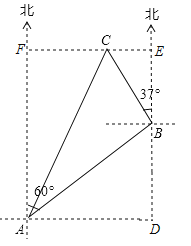
【解析】试题解析:辅助线如图所示:BD⊥AD,BE⊥CE,CF⊥AF,在Rt△ABD中,根据勾股定理可求AD,在Rt△BCE中,根据三角函数可求CE,EB,在Rt△AFC中,根据勾股定理可求AC,再根据路程÷时间=速度求解即可.
试题解析:解:辅助线如图所示:
BD⊥AD,BE⊥CE,CF⊥AF,有题意知,∠FAB=60°,∠CBE=37°,∴∠BAD=30°,∵AB=20海里,∴BD=10海里,在Rt△ABD中,AD=![]() =
=![]() ≈17.32海里,在Rt△BCE中,sin37°=
≈17.32海里,在Rt△BCE中,sin37°=![]() ,∴CE=BCsin37°≈0.6×10=6海里,∵cos37°=
,∴CE=BCsin37°≈0.6×10=6海里,∵cos37°=![]() ,∴EB=BCcos37°≈0.8×10=8海里,EF=AD=17.32海里,∴FC=EF﹣CE=11.32海里,AF=ED=EB+BD=18海里,在Rt△AFC中,AC=
,∴EB=BCcos37°≈0.8×10=8海里,EF=AD=17.32海里,∴FC=EF﹣CE=11.32海里,AF=ED=EB+BD=18海里,在Rt△AFC中,AC=![]() =
=![]() ≈21.26海里,21.26×3≈64海里/小时.
≈21.26海里,21.26×3≈64海里/小时.
答:救援的艇的航行速度大约是64海里/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图.
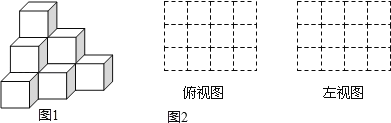
(2)用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 、
、 、
、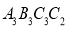 …按如图所示的方式放置.点
…按如图所示的方式放置.点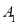 、
、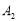 、
、 …和点
…和点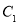 、
、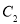 、
、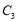 …别在直线
…别在直线 和
和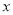 轴上,则点
轴上,则点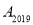 的坐标是( )
的坐标是( )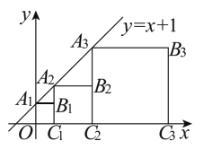
A.
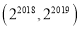 B.
B.  C.
C. 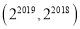 D.
D. 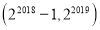
-
科目: 来源: 题型:
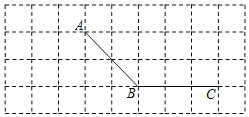
查看答案和解析>>【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD; 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E; 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F; 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;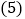 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______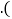 用“
用“ ”连接
”连接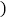
-
科目: 来源: 题型:
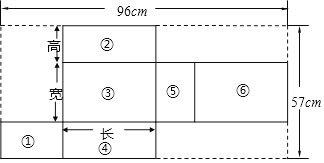
查看答案和解析>>【题目】如图是某涌泉蜜桔长方体包装盒的展开图.具体数据如图所示,且长方体盒子的长是宽的2倍.
(1)展开图的6个面分别标有如图所示的序号,若将展开图重新围成一个包装盒,则相对的面分别是 与 , 与 , 与 ;
(2)若设长方体的宽为xcm,则长方体的长为 cm,高为 cm;(用含x的式子表示)
(3)求这种长方体包装盒的体积.
-
科目: 来源: 题型:
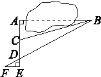
查看答案和解析>>【题目】数学课外兴趣小组的同学们要测量被池塘隔开的两棵树A,B之间的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到点E处,再从点E沿着垂直于AE的方向走到点F处,C为AE上一点,其中三位同学分别测得三组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A,B两树之间的距离的有________组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生本学期6次数学考试成绩如下表所示:
成绩类别
第一次月考
第二次月考
期中
第三次月考
第四次月考
期末
成绩/分
105
110
108
113
108
112
(1)6次考试成绩的中位数为 ,众数为 .
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
相关试题

