【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
参考答案:
【答案】C
【解析】因为∠BAC和∠ABC的平分线相交于点O,所以∠OBA=![]() ∠CBA, ∠OAB=
∠CBA, ∠OAB=![]() ∠CAB,所以∠AOB=
∠CAB,所以∠AOB=![]() ∠CBA-
∠CBA-![]() ∠CAB=
∠CAB=![]() =90°+
=90°+ ![]() , ①正确,
, ①正确,
因为EF∥AB,所以∠FOB=∠ABO,又∠ABO=∠FBO,所以∠FOB=∠FBO,所以FO=FB,
同理EO=EA,所以AE+BF=EF, ②正确,
当∠C=![]() 时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
作OH⊥AC于H,
因为∠BAC和∠ABC的平分线相交于点O,所以点O在∠C的平分线上,
所以OD=OH,所以S△CEF= ![]() , ④正确,
, ④正确,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊数学家把数1,3,6,10,15,21,……叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1 ,第二个三角数形记为a 2 ,……,第n个三角形数记为an,计算a2-a1,a 3-a2……由此推算a 100-a 99 =________;a100=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为
 的中点.
的中点.
(1)求证:AB=BC.
(2)试判断四边形BOCD的形状,并说明理由.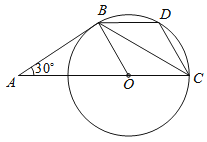
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB交弦ED于点G,EG=DG,⊙O的切线BC交DO的延长线于点C,F是DC与⊙O的交点,连结AF.
(1)求证:DE∥BC;
(2)若OD=1,CF= , 求AF的长.
, 求AF的长.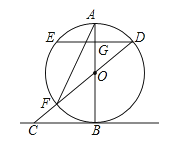
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
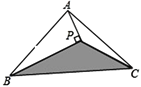
A. 3cm2 B. 4cm2 C. 5cm2 D. 6cm2
-
科目: 来源: 题型:
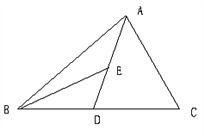
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?
相关试题

