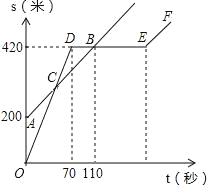
【题目】巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;
(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;
(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
参考答案:
【答案】(1)t,s;(2)2,6;(3)小明距起点的距离为300米.
【解析】
解析
(1)观察函数图象即可找出谁是自变量谁是因变
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)设t秒时,小明第一次追上朱老师,列出关系式即可解答
解:(1)在上述变化过程中,自变量是t,因变量是s;
(2)朱老师的速度![]() =2(米/秒),小明的速度为
=2(米/秒),小明的速度为![]() =6(米/秒);
=6(米/秒);
故答案为t,s;2,6;
(3)设t秒时,小明第一次追上朱老师
根据题意得6t=200+2t,解得t=50(s),
则50×6=300(米),
所以当小明第一次追上朱老师时,小明距起点的距离为300米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线
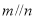 ,点
,点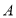 ,
,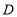 在直线
在直线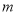 上,点
上,点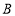 ,
,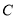 在直线
在直线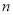 上,且AB//CD,若
上,且AB//CD,若 保持不动,线段
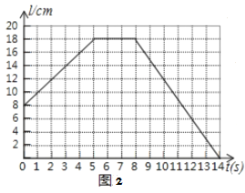
保持不动,线段 先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了
先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了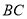 的长度
的长度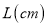 随时间
随时间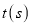 的变化而变化的情况,则
的变化而变化的情况,则(1)在线段
 开始平移之前,
开始平移之前,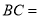 _______
_______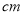 ;
;(2)线段
 边向右平移了_______
边向右平移了_______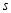 ,向右平移的速度是______
,向右平移的速度是______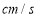 ;
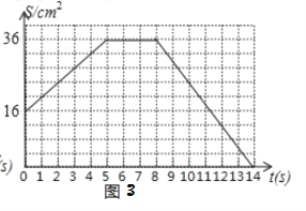
;(3)图3反映了变化过程中
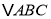 的面积
的面积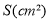 随时间
随时间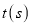 变化的情况.
变化的情况.①平行线
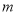 ,
,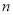 之间的距离为_______
之间的距离为_______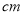 ;
;②当
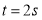 时,面积S的值为_____
时,面积S的值为_____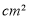 ;
;③当
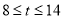 时,直接写出
时,直接写出 关于
关于 的函数关系式______(可以不化简).
的函数关系式______(可以不化简).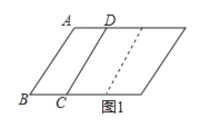
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某花园护栏是用直径为
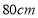 的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加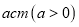 ,设半圆形条钢的个数为
,设半圆形条钢的个数为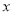 (
(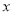 为正整数),护栏总长度为
为正整数),护栏总长度为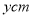 .
.(1)若
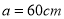 .
.①当
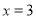 时,y=______
时,y=______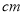 ;
;②写出
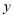 与
与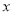 之间的函数关系式为_______.
之间的函数关系式为_______.(2)若护栏总长度为
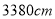 ,则当
,则当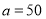 时,所用半圆形条钢个数为_______;
时,所用半圆形条钢个数为_______;(3)若护栏总长度不变,则当
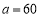 时,用了
时,用了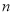 个半圆形条钢;当
个半圆形条钢;当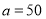 时,用了
时,用了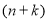 个半圆形条钢.请求出
个半圆形条钢.请求出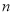 与
与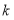 之间的关系式.
之间的关系式.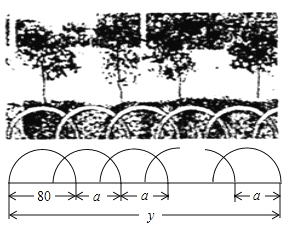
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A. 13B. 14C. 15D. 16
-
科目: 来源: 题型:
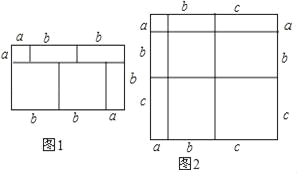
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1,可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形、3张边长为b的正方形、5张边长为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,求9x+10y+6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点G,E、F分别是边AD、BC的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )

A. 点CB. 点EC. 点FD. 点G
相关试题

