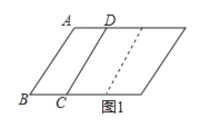
【题目】如图1,已知直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,且AB//CD,若
上,且AB//CD,若![]() 保持不动,线段
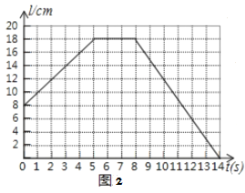
保持不动,线段![]() 先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了
先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了![]() 的长度
的长度![]() 随时间
随时间![]() 的变化而变化的情况,则
的变化而变化的情况,则
(1)在线段![]() 开始平移之前,
开始平移之前,![]() _______
_______![]() ;
;
(2)线段![]() 边向右平移了_______
边向右平移了_______![]() ,向右平移的速度是______
,向右平移的速度是______![]() ;
;
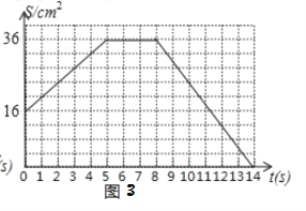
(3)图3反映了变化过程中![]() 的面积
的面积![]() 随时间
随时间![]() 变化的情况.
变化的情况.
①平行线![]() ,
,![]() 之间的距离为_______
之间的距离为_______![]() ;
;
②当![]() 时,面积S的值为_____
时,面积S的值为_____![]() ;
;
③当![]() 时,直接写出
时,直接写出![]() 关于
关于![]() 的函数关系式______(可以不化简).
的函数关系式______(可以不化简).
参考答案:
【答案】(1)8;(2)5,2;(3)①4;②24;③S=-6t+84(8≤t≤14).
【解析】
(1)根据CD从t=0时开始平移,在图2中找出对应的L的值即可得BC的长;
(2)由图2可得线段CD平移5s时BC的长增加了10cm,可得到中间停止时的平移距离,根据速度=距离÷时间即可得平移速度;
(3)①设m、n之间的距离为x,由图2、图3可知BC=8时,△ABC的面积为16,根据三角形的面积公式即可求出x的值,可得答案;
②由题2可知t=2时,BC=12,利用三角形面积公式即可求出S的值;
③由图2可知向左平移的距离为18cm,可求出平移速度,根据平移时间为(t-8)s,利用三角形面积公式即可得答案.
(1)∵CD开始平移时,t=0,
∴由图2可知:t=0时,L=8,
∴在线段![]() 开始平移之前,
开始平移之前,![]() 8cm,
8cm,
故答案为:8
(2)∵t为5到8s时,L的长不变,
∴CD运动到5s时停止,即CD向右平移了5s,
∵t=5时,L=18,
∴CD平移的距离为18-8=10cm,
∴CD向右平移的速度为10÷5=2cm/s,
故答案为:5,2
(3)①设m、n之间的距离为xcm,
由图2和图3可知:CD平移前BC=8,S=16,
∴S=![]() BC·x=16,
BC·x=16,
解得:x=4,即m、n之间的距离为4cm,
故答案为:4
②由图2可知:t=2时,BC=12,
∴S=![]() ×4BC=
×4BC=![]() ×4×12=24cm2,
×4×12=24cm2,
故答案为:24
③由图2、图3可知,向左平移的距离为18cm,平移的时间为6s,
∴向左平移的速度为18÷6=3cm/s,
∴S=![]() ×[18-3(t-8)]×4=-6t+84(8≤t≤14).
×[18-3(t-8)]×4=-6t+84(8≤t≤14).
故答案为:S=-6t+84(8≤t≤14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当
 很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率
很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率 .
.(2)试估算盒子里白、黑两种颜色的球各有多少只?
(3)在(2)条件下如果要使摸到白球的概率为
 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B. 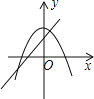 C.
C. 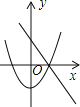 D.
D. 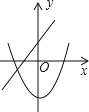
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某花园护栏是用直径为
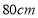 的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加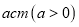 ,设半圆形条钢的个数为
,设半圆形条钢的个数为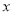 (
(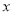 为正整数),护栏总长度为
为正整数),护栏总长度为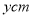 .
.(1)若
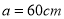 .
.①当
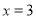 时,y=______
时,y=______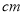 ;
;②写出
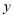 与
与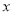 之间的函数关系式为_______.
之间的函数关系式为_______.(2)若护栏总长度为
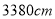 ,则当
,则当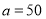 时,所用半圆形条钢个数为_______;
时,所用半圆形条钢个数为_______;(3)若护栏总长度不变,则当
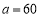 时,用了
时,用了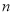 个半圆形条钢;当
个半圆形条钢;当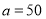 时,用了
时,用了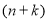 个半圆形条钢.请求出
个半圆形条钢.请求出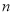 与
与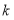 之间的关系式.
之间的关系式.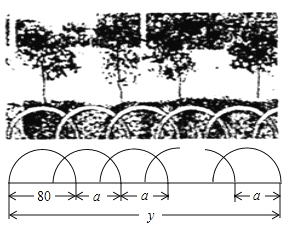
-
科目: 来源: 题型:
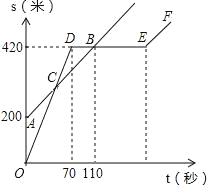
查看答案和解析>>【题目】巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;
(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;
(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
相关试题

