【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…
把上述探究的结果进行整理,列表如下:
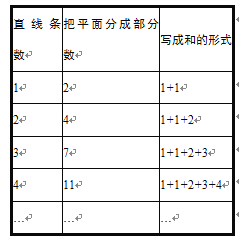
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式为 ;
(2)当直线条数为10时,把平面最多分成 部分;
(3)当直线条数为n时,把平面最多分成几部分?
参考答案:
【答案】(1)16,1+1+2+3+4 (2)56 ; (3)![]()
【解析】试题分析:(1)根据表中数据,得出规律,直接写出答案即可;(2)根据表中数据,得出规律,直接写出答案即可;(3)根据表中数据,总结规律即可.
试题解析:
(1)16,+1+2+3+4+5=16;
(2)1+1+2+3+…+10=56;
(3)当直线条数为n时,设最多把平面分成m部分,则有以下规律:
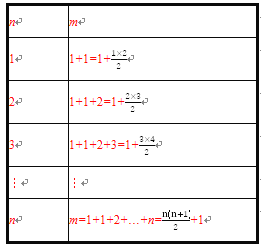
所以当直线条数为n时,可把平面最多分成![]() 部分.
部分.
-
科目: 来源: 题型:
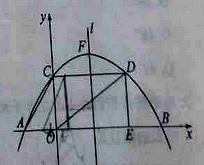
查看答案和解析>>【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2+4x﹣2配方成y=(x﹣h)2+k的形式,则y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2﹣3x+c=0有一个根为1,该方程的另一个根为_____.
-
科目: 来源: 题型:
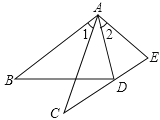
查看答案和解析>>【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
相关试题

