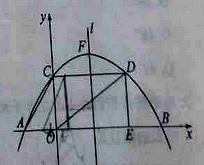
【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
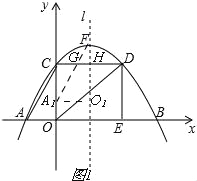
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
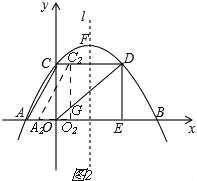
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
参考答案:
【答案】(1)、D(6,4);y=﹣![]() x2+
x2+![]() x+4;(2)、
x+4;(2)、![]() ;(3)、当0<t≤3时,S=
;(3)、当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12
t2﹣3t+12
【解析】
试题分析:(1)、用待定系数法求抛物线解析式;(2)、由GH∥A1O1,求出GH=1,再求出FH,S重叠部分=S△A1O1F﹣S△FGH计算即可;(3)、分两种情况①直接用面积公式计算,②用面积差求出即可.
试题解析:(1)、∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).
∴设抛物线的解析式为y=a(x+3)(x﹣9), ∵C(0,4)在抛物线上, ∴4=﹣27a,
∴a=﹣![]() , ∴设抛物线的解析式为y=﹣
, ∴设抛物线的解析式为y=﹣![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣![]() x2+
x2+![]() x+4,
x+4,
∵CD垂直于y轴,C(0,4) ∴﹣![]() x2+
x2+![]() x+4=4, ∴x=6, ∵D(6,4),
x+4=4, ∴x=6, ∵D(6,4),
(2)、如图1, ∵点F是抛物线y=﹣![]() x2+
x2+![]() x+4的顶点,∴F(3,
x+4的顶点,∴F(3,![]() ), ∴FH=
), ∴FH=![]() ,
,
∵GH∥A1O1, ∴![]() , ∴
, ∴![]() , ∴GH=1,
, ∴GH=1,
∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG,
∴S重叠部分=S△A1O1F﹣S△FGH=![]() A1O1×O1F﹣
A1O1×O1F﹣![]() GH×FH=
GH×FH=![]() ×3×4﹣
×3×4﹣![]() ×1×
×1×![]() =
=![]() .
.
(3)、①当0<t≤3时,如图2, ∵C2O2∥DE, ∴![]() , ∴
, ∴![]() , ∴O2G=
, ∴O2G=![]() t,
t,
∴S=S△OO2G=![]() OO2×O2G=
OO2×O2G=![]() t×
t×![]() t=
t=![]() t2,
t2,
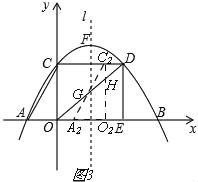
②当3<t≤6时,如图3, ∵C2H∥OC, ∴![]() , ∴
, ∴![]() , ∴C2H=
, ∴C2H=![]() (6﹣t),
(6﹣t),
∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH=![]() OA×OC﹣
OA×OC﹣![]() C2H×(t﹣3)=
C2H×(t﹣3)=![]() ×3×4﹣
×3×4﹣![]() ×
×![]() (6﹣t)(t﹣3)=
(6﹣t)(t﹣3)=![]() t2﹣3t+12
t2﹣3t+12
∴当0<t≤3时,S=![]() t2,当3<t≤6时,S=
t2,当3<t≤6时,S=![]() t2﹣3t+12.
t2﹣3t+12.
-
科目: 来源: 题型:
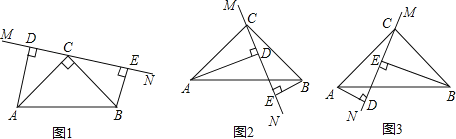
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,
BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请写出DE、AD、BE之间的等量关系并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE之间又有怎样的等量关系?请直接写出结论.
-
科目: 来源: 题型:
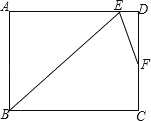
查看答案和解析>>【题目】(2016广西省贺州市第18题)在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在演唱比赛中,5位评委给一位歌手的打分如下:8.2分,8.3分,7.8分,7.7分,8.0分,则这位歌手的平均得分是分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…
把上述探究的结果进行整理,列表如下:
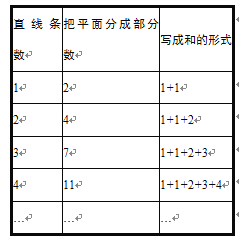
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式为 ;
(2)当直线条数为10时,把平面最多分成 部分;
(3)当直线条数为n时,把平面最多分成几部分?
相关试题

