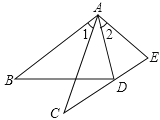
【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
参考答案:
【答案】 ①②③, ④.
【解析】根据全等三角形的判定方法进行组合、证明,答案不唯一.
解;答案不唯一.如:
已知:在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2.
求证:∠B=∠C.
证明:∵∠1=∠2,
∴∠BAD=∠CAE.
在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠B=∠C(全等三角形对应角相等);
故答案为:①②③,④.
∵∠1=∠2,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成7部分…
把上述探究的结果进行整理,列表如下:
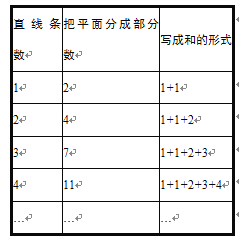
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式为 ;
(2)当直线条数为10时,把平面最多分成 部分;
(3)当直线条数为n时,把平面最多分成几部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2+4x﹣2配方成y=(x﹣h)2+k的形式,则y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2﹣3x+c=0有一个根为1,该方程的另一个根为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向右平移3个单位,再向下平移4个单位后所得到的抛物线解析式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图所示的图形,写出下列问题的结果:

(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系?
相关试题

