【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
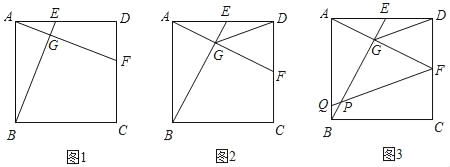
(1)写出BE与AF之间的关系,并证明你的结论;
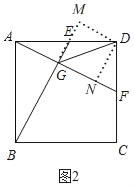
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长;
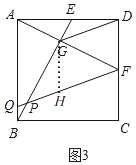
(3)如图3,在(2)的条件下,作FQ∥DG交AB于点Q,请直接写出FQ的长.
参考答案:
【答案】(1)BE=AF,BE⊥AF;(2)GD是∠EGF的角平分线,证明见解析,GD=![]() ;(3)FQ=
;(3)FQ=![]() .
.
【解析】
(1)根据已知条件可先证明△BAE≌△ADF,得到BE=AF,再由角的关系得到∠AGE=90°从而证明BE⊥AF;
(2)过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,根据勾股定理和三角形的面积相等求出DN,然后证明△AEG≌△DEM,得到DN=DM,再根据角平分线的性质可证明GD平分∠EGF,进而在等腰直角三角形中求得GD;
(3)过点G作GH∥AQ交FQ于H,可得到四边形DFHG是平行四边形,进而可得△FGH∽△FAQ,然后根据三角形相似的性质可求得FQ.
解:(1)BE=AF,BE⊥AF,理由:
四边形ABCD是正方形,
∴BA=AD=CD,∠BAE=∠D=90°,
∵DE=CF,
∴AE=DF,
∴△BAE≌△ADF(SAS),
∴BE=AF,∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AGE=90°,
∴BE⊥AF
(2)如图2,过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,
在Rt△ADF中,根据勾股定理得,AF=![]() ,
,
∵S△ADF=![]() AD×FD=
AD×FD=![]() AF×DN,
AF×DN,
∴DN=![]() ,
,
∵△BAE≌△ADF,
∴S△BAE=S△ADF,
∵BE=AF,
∴AG=DN,
∵AE=DE,∠MED=∠AEG,∠DME=∠AGM,
∴△AEG≌△DEM(AAS),
∴AG=DM,
∴DN=DM,
∵DM⊥BE,DN⊥AF,
∴GD平分∠MGN,即GD平分∠EGF,
∴∠DGN=![]() ∠MGN=45°,
∠MGN=45°,
∴△DGN是等腰直角三角形,
∴GD=![]() DN=
DN=![]() ;
;
(3)如图3,由(2)知,GD=![]() ,AF=
,AF=![]() ,AG=DN=
,AG=DN=![]() ,
,
∴FG=AF﹣AG=![]() ,
,
过点G作GH∥AQ交FQ于H,
∴GH∥DF,
∵FQ∥DG,
∴四边形DFHG是平行四边形,
∴FH=DG=![]() ,
,
∵GH∥AQ,
∴△FGH∽△FAQ,
∴![]() ,
,
∴![]() ,
,
∴FQ=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
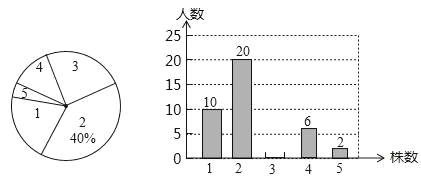
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
-
科目: 来源: 题型:
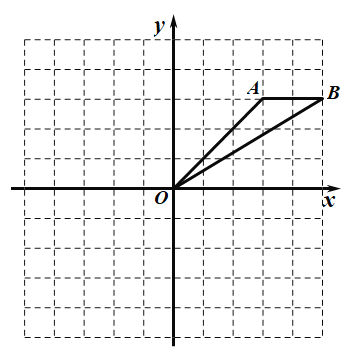
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(3,3),B(5,3).
(1)已知点C(2,-4),求四边形AOCB的面积;
(2)将线段OB先向上平移2个单位长度,再向左平移4个单位长度,得到线段O2B2,画出两次平移后的图形,并求线段OB在两次平移过程中扫过的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=kx﹣2k(k<0),与y轴交于点A,与x轴交于点B,AB=2
 .
.
(1)直接写出点A,点B的坐标;
(2)如图2,以AB为边,在第一象限内画出正方形ABCD,求直线DC的解析式;
(3)如图3,(2)中正方形ABCD的对角线AC、BD即交于点G,函数y=mx和y=
 (x≠0)的图象均经过点G,请利用这两个函数的图象,当mx>
(x≠0)的图象均经过点G,请利用这两个函数的图象,当mx> 时,直接写出x的取值范围.
时,直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,
 =3,n=
=3,n=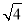 ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.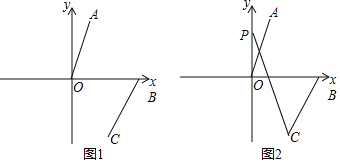
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=﹣
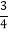 x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.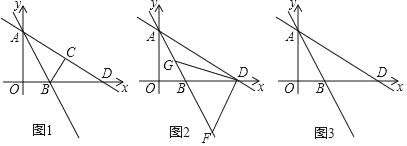
(1)求点B的坐标;
(2)如图2,直线AB上的两点F、G,△DFG是以FG为斜边的等腰直角三角形,求点G的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P、Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=7,其中点E为CD的中点.有一动点P,从点A按A→B→C→E的顺序在矩形ABCD的边上移动,移动到点E停止,在此过程中以点A,P,E三点为顶点的直角三角形的个数为( )
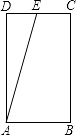
A.2
B.3
C.4
D.5
相关试题

