【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
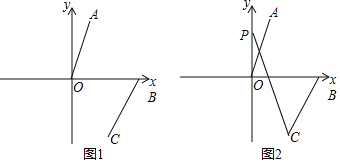
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
参考答案:
【答案】(1)A(1,3); B(3,0);(2)S四边形AOCB=9;(3)∠BCP﹣∠CPO=90°﹣a.
【解析】
(1)根据算术平方根、二次根式和偶次幂解答即可;
(2)根据平移的性质和三角形的面积解答即可;
(3)过点P作PD∥OA,可证得PD∥OA∥BC,由平行线的性质进行解答即可.
(1)∵a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
∴m=﹣3,n=2,a=3,b=3,
∴A(1,3),B(3,0);
故答案为:A(1,3); B(3,0);
(2)如图1所示:
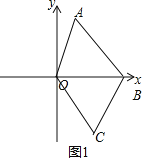
由题意知:C(2,﹣3),
∵B(3,0),
∴OB=3,
∴S四边形AOCB=S△AOB+S△BOC=![]() ,
,
故答案为:9;
(3)过点P作PD∥OA,如图2所示:

∵OA∥BC,
∴PD∥OA∥BC
∴∠BCP=∠DPC,∠DPO=∠AOP.
∵∠AOB=a,
∴∠AOP=90°﹣∠AOB=90°﹣a.
∴∠DPO=90°﹣a.
∵∠DPC=∠DPO+∠CPO,
∴∠BCP=∠CPO+90°﹣a,
即∠BCP﹣∠CPO=90°﹣a,
故答案为:∠BCP﹣∠CPO=90°﹣a.
-
科目: 来源: 题型:
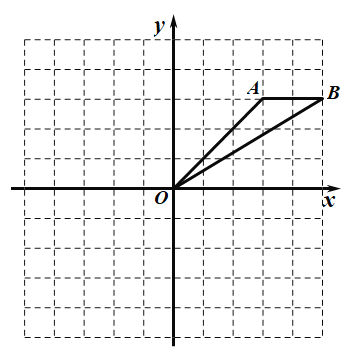
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(3,3),B(5,3).
(1)已知点C(2,-4),求四边形AOCB的面积;
(2)将线段OB先向上平移2个单位长度,再向左平移4个单位长度,得到线段O2B2,画出两次平移后的图形,并求线段OB在两次平移过程中扫过的总面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=kx﹣2k(k<0),与y轴交于点A,与x轴交于点B,AB=2
 .
.
(1)直接写出点A,点B的坐标;
(2)如图2,以AB为边,在第一象限内画出正方形ABCD,求直线DC的解析式;
(3)如图3,(2)中正方形ABCD的对角线AC、BD即交于点G,函数y=mx和y=
 (x≠0)的图象均经过点G,请利用这两个函数的图象,当mx>
(x≠0)的图象均经过点G,请利用这两个函数的图象,当mx> 时,直接写出x的取值范围.
时,直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
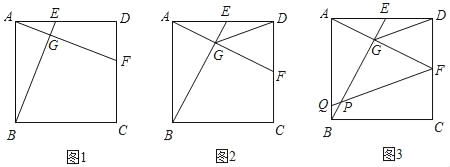
(1)写出BE与AF之间的关系,并证明你的结论;
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长;
(3)如图3,在(2)的条件下,作FQ∥DG交AB于点Q,请直接写出FQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=﹣
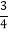 x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.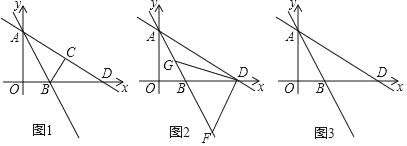
(1)求点B的坐标;
(2)如图2,直线AB上的两点F、G,△DFG是以FG为斜边的等腰直角三角形,求点G的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P、Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=7,其中点E为CD的中点.有一动点P,从点A按A→B→C→E的顺序在矩形ABCD的边上移动,移动到点E停止,在此过程中以点A,P,E三点为顶点的直角三角形的个数为( )
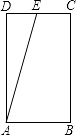
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
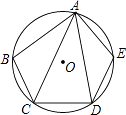
查看答案和解析>>【题目】如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=°.
相关试题

