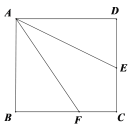
【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2 ![]() ,则△BDG的面积为 .
,则△BDG的面积为 . 
参考答案:
【答案】96
【解析】解:过点E作EH⊥AC,垂足为H,连接AE. 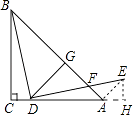
∵∠BDE=90°,
∴∠BDC+∠EDH=90°.
又∵∠CBD+∠CDB=90°,
∴∠CBD=∠EDH.
在△BCD和△DHE中, 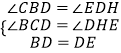 ,
,
∴△BCD≌△DHE.
∴BC=DH,CD=EH=2 ![]() .
.
∵△ABC为等腰直角三角形,
∴BC=CA.
∴AC=DH.
∴DC=AH=2 ![]() .
.
∴AH=EH=2 ![]() .
.
∴AE= ![]() =4.
=4.
∵∠BAC=45°,∠EAH=45°,
∴∠FAE=90°.
∴AF= ![]() =3.
=3.
∵∠BDF=∠FAE,∠BFD=∠EFA,
∴△BDF∽△EFA.
∴ ![]() .
.
设DF=x,则BD=DE=x+5.
∴ ![]() .
.
解得:x=15.
∴DF=15,BD=20.
∴BG= ![]() BD=16,DG=
BD=16,DG= ![]() =12.
=12.
∴ ![]() =
= ![]() =96.
=96.
故答案为;96.
过点E作EH⊥AC,垂足为H,连接AE.先依据AAS证明△BCD≌△DHE,从而得到BC=DH,CD=EH=2 ![]() ,由等腰直角三角形的性质可知BC=CA,从而可证明AH=EH=2
,由等腰直角三角形的性质可知BC=CA,从而可证明AH=EH=2 ![]() ,由勾股定理可知AE=4.在△EFA中由勾股定理可求得AF=3,由∠BDF=∠FAE,∠BFD=∠EFA可知△BDF∽△EFA,设DF=x,则BD=DE=x+5由相似三角形的性质可知:
,由勾股定理可知AE=4.在△EFA中由勾股定理可求得AF=3,由∠BDF=∠FAE,∠BFD=∠EFA可知△BDF∽△EFA,设DF=x,则BD=DE=x+5由相似三角形的性质可知: ![]() .解得:x=15.故此DF=15,BD=20,从而可求得BG=
.解得:x=15.故此DF=15,BD=20,从而可求得BG= ![]() BD=16,DG=
BD=16,DG= ![]() =12,最后依据三角形的面积公式求解即可.
=12,最后依据三角形的面积公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PB+PC的长最短.
-
科目: 来源: 题型:
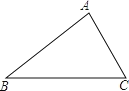
查看答案和解析>>【题目】如图,△ABC中,∠A=84°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ABP=15°,求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题.

(1)①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
(2)直接写出点A2 , B2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分).

(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,
求证:AF=AD+CF.
相关试题

