【题目】某公司在![]() 两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从
两地分别库存有挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从![]() 地运一台到甲、乙两地的费用分别是500元和400元;从
地运一台到甲、乙两地的费用分别是500元和400元;从![]() 地运一台到甲、乙两地费用分别是300元和600元,设从
地运一台到甲、乙两地费用分别是300元和600元,设从![]() 地运往甲地
地运往甲地![]() 台挖掘机.
台挖掘机.
(1)请补全下表,并求出运这批挖掘机的总费用是多少?
甲 | 乙 | 总计 | |
|
| ____________台 | 16台 |
| _______________台 | ____________台 | 12台 |
总计 | 15台 | 13台 | 28台 |
(2)当从![]() 地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
地运往甲地5台挖掘机时,运这批挖掘机的总费用是多少?
(3)怎样安排运输方案,可使运这批挖掘机的总费用最少,最少费用是多少?
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;
;![]() 元;(2)总费用是11100元;(3)
元;(2)总费用是11100元;(3)![]() 地运往甲3台,运往乙13台,
地运往甲3台,运往乙13台,![]() 地运往甲12台时,总运费最少,最少运费为:10300元.
地运往甲12台时,总运费最少,最少运费为:10300元.
【解析】
(1)直接根据条件补全表格,然后根据运送挖掘机的总费用=A地运往甲的费用+B地运往甲的费用+A地运往乙的费用+B地运往乙的费用,列式计算即可;
(2)把x=5代入(1)中求得的式子计算即可;
(3)根据(1)中总费用的式子分析当x的值发生变化时的变化规律,即可求出最小费用.
解:(1)∵A有挖掘机16台,运往甲x台,
∴A运往乙(16-x)台,B运往甲(15-x)台,
∵B有挖掘机12台,
∴B运往乙12-(15-x)=(x-3)台;
总费用为:![]()
![]()
=![]() (元);
(元);
故答案是:![]() ,
,![]() ,
,![]() ;
;![]() 元
元
(2)当![]() 时,
时,![]() (元),
(元),
即从![]() 地运往甲地5台挖掘机时,运这批挖掘机的总费用是11100元.
地运往甲地5台挖掘机时,运这批挖掘机的总费用是11100元.
(3)因为总费用为![]() 元,所以
元,所以![]() 越小,总运费就越少,
越小,总运费就越少,
又因为运输的台数不能是负数,所以![]() 最小取3,
最小取3,
即![]() 地运往甲3台,运往乙13台,
地运往甲3台,运往乙13台,![]() 地运往甲12台时,总运费最少,
地运往甲12台时,总运费最少,
最少运费为:![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,把△ABC沿对角线AC折叠,得到△AB'C,B'C与AD相交于点E,则AE的长________.
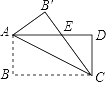
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=
 BM.
BM.(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG= .
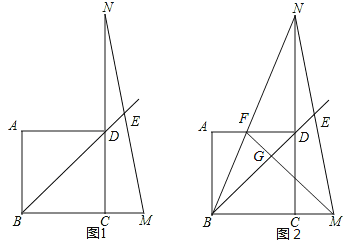
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD的周长是32 cm,
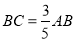 ,
,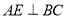 ,
,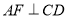 ,E,F是垂足,且
,E,F是垂足,且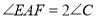
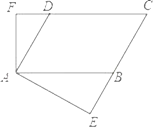
(1)求
 的度数;
的度数;(2)求BE,DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
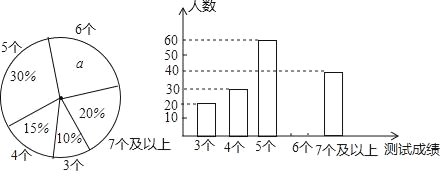
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a= %,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、 个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

相关试题

