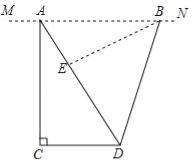
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离(![]() 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米)

参考答案:
【答案】2.7.
【解析】试题分析:如图,过B作BE⊥AD于E,根据三角形的内角和定理可求得∠ADB=45°,根据直角三角形的性质得到AE=2.BE=2![]() ,求得AD=2+2
,求得AD=2+2![]() ,即可得到结论.
,即可得到结论.
试题解析:过B作BE⊥AD于E,
∵∠NAD=60°,∠ABD=75°,
∴∠ADB=45°,
∵AB=6×![]() =4,
=4,
∴AE=2.BE=2![]() ,
,
∴DE=BE=2![]() ,
,
∴AD=2+2![]() ,
,
∵∠C=90,∠CAD=30°,
∴CD=![]() AD=1+
AD=1+![]() ≈2.7.
≈2.7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为:
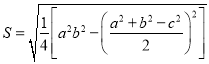 ①(其中
①(其中 为三角形的三边长,
为三角形的三边长, 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”; ……②(其中
……②(其中 )
)材料二:对于平方差公式:
 公式逆用可得:
公式逆用可得: ,例:
,例:
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:

(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,正方形
 的两边分别在正方形
的两边分别在正方形 的边
的边 和
和 上,连接
上,连接 .填空:线段
.填空:线段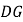 与
与 的数量关系为________;直线
的数量关系为________;直线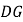 与
与 所夹锐角的大小为________.
所夹锐角的大小为________.


(2)如图②,将正方形
 绕点
绕点 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.(3)把图②中的正方形都换成菱形,且
 ,如图③,直接写出
,如图③,直接写出 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:基本不等式
 ≤
≤ (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.例如:在x>0的条件下,当x为何值时,x+
 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵x>0,
 >0∴
>0∴ ≥
≥ 即是x+
即是x+ ≥2
≥2
∴x+
 ≥2
≥2当且仅当x=
 即x=1时,x+
即x=1时,x+ 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+
 ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.(2)当x>0时,式子x2+1+
 ≥2成立吗?请说明理由.
≥2成立吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x
…
﹣2
﹣1
0
1
2
3
…
﹣x2+bx+c
…
5
n
c
2
﹣3
﹣10
…
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
相关试题

