【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
参考答案:
【答案】(1)x=![]() 时,有最小值,最小值为2
时,有最小值,最小值为2![]() ;(2)式子不成立,见解析.
;(2)式子不成立,见解析.
【解析】
(1)将原式变形为2x+![]() ≥2
≥2![]() 后,结合材料即可解决问题;
后,结合材料即可解决问题;
(2)将原式变形为x2+1+![]() ≥2
≥2![]() 后,结合材料及x>0即可作出判断.
后,结合材料及x>0即可作出判断.
解:(1)∵x>0,
∴2x>0,
∴2x+![]() ≥2
≥2![]() =2
=2![]() ,
,
当且仅当2x=![]() 即x=
即x=![]() 时,2x+
时,2x+![]() 有最小值,最小值为2
有最小值,最小值为2![]() .
.
(2)式子不成立.
理由:∵x>0,
∴x2+1>0,![]() >0,
>0,
∴x2+1+![]() ≥2
≥2![]() =2,
=2,
当且仅当x2+1=![]() 即x=0时,不等式成立,
即x=0时,不等式成立,
∵x>0,
∴不等式不能取等号,即不成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离(
 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,正方形
 的两边分别在正方形
的两边分别在正方形 的边
的边 和
和 上,连接
上,连接 .填空:线段
.填空:线段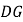 与
与 的数量关系为________;直线
的数量关系为________;直线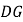 与
与 所夹锐角的大小为________.
所夹锐角的大小为________.


(2)如图②,将正方形
 绕点
绕点 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.(3)把图②中的正方形都换成菱形,且
 ,如图③,直接写出
,如图③,直接写出 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x
…
﹣2
﹣1
0
1
2
3
…
﹣x2+bx+c
…
5
n
c
2
﹣3
﹣10
…
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

