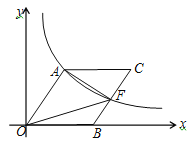
【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,OA =10,sin∠AOB =![]() ,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.
,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)求反比例函数的表达式;
(2)若点F为BC的中点,求△OBF的面积.
参考答案:
【答案】(1)y=![]() (x>0);(2)18
(x>0);(2)18
【解析】(1)先过点A作AH⊥OB,根据sin∠AOB=![]() ,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
(2)过点F作FM⊥x轴于M,由四边形AOBC是平行四边形得∠AOB=∠FBM,故sin∠FBM=![]() ,因点F为BC的中点,所以BF=5,得FM=4,BM=3,得S△BFM=6,因为点F在反比例函数图象上,故S△OFM=24,根据S△OBF=S△OFM-S△BFM可求出结果.
,因点F为BC的中点,所以BF=5,得FM=4,BM=3,得S△BFM=6,因为点F在反比例函数图象上,故S△OFM=24,根据S△OBF=S△OFM-S△BFM可求出结果.
(1)过点A作AH⊥OB于H
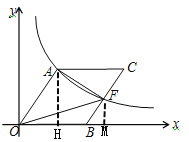
∵sin∠AOB=![]() ,OA=10
,OA=10
∴AH=8,OH=6
∴A点坐标为(6,8)
∵反比例函数y=kx(k>0)过(3,4)
可得:k=48
∴反比例函数解析式:y=![]() (x>0)
(x>0)
(2)过点F作FM⊥x轴于M
∵四边形AOBC是平行四边形,
∴AO∥BC,AO=CB=10 ∴∠AOB=∠FBM
∵sin∠AOB=![]()
∴sin∠FBM=![]()
∵点F为BC的中点,
∴BF=5,
∴FM=4,BM=3,
∴S△BFM=6
∵F在反比例函数图象上,
∴S△OFM=24
∴S△OBF=S△OFM-S△BFM=18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,D,E是
,D,E是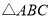 内两点,AD平分
内两点,AD平分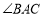 ,∠EBC=∠E=60°,若
,∠EBC=∠E=60°,若 ,DE=2,则BC的长为( )
,DE=2,则BC的长为( )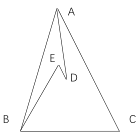
A.4B.6C.8D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家今年种植的“夏黑”葡萄喜获丰收,采摘上市后若干天便全部销完.小明对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(千克)与上市时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少15千克.
(1)第16天的日销售量是 千克.
(2)求y与x之间的函数关系式,并写出x的取值范围;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
(1)求证:BD平分∠PBC;
(2)若PD =3DE,求
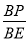 的值.
的值.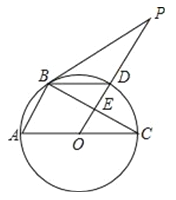
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.垂美四边形有如下性质:
垂美四边形的两组对边的平方和相等.
已知:如图1,四边形ABCD是垂美四边形,对角线AC、BD相交于点E.
求证:AD2+BC2=AB2+CD2
证明:∵四边形ABCD是垂美四边形
∴AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2.
拓展探究:
(1)如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
问题解决:
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5.求GE长.
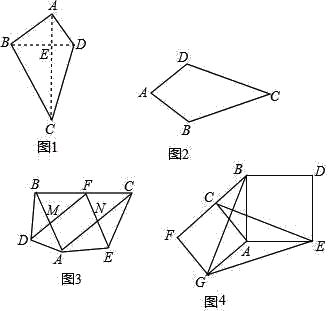
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y =ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.点P、Q分别是AB、BC上的动点,当点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动.设P、Q同时运动的时间为t秒(0<t<2).
(1)求抛物线的表达式;
(2)设△PBQ的面积为S ,当t为何值时,△PBQ的面积最大,最大面积是多少?
(3)当t为何值时,△PBQ是等腰三角形?
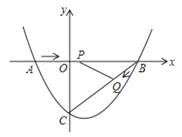
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从圆形跑道(圆形跑道的总长小于700m)上一直径两端A,B相向起跑.第一次相遇时离A点100m,第二次相遇时离B点60m,则圆形跑道的总长为( )
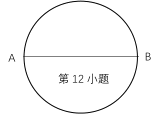
A.240mB.360mC.480mD.600m
相关试题

