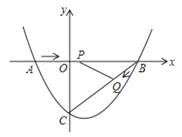
【题目】如图,在平面直角坐标系中,抛物线y =ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.点P、Q分别是AB、BC上的动点,当点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动.设P、Q同时运动的时间为t秒(0<t<2).
(1)求抛物线的表达式;
(2)设△PBQ的面积为S ,当t为何值时,△PBQ的面积最大,最大面积是多少?
(3)当t为何值时,△PBQ是等腰三角形?
参考答案:
【答案】(1)y=![]() x2
x2![]() x3;(2)当t=1时,S△PBQ最大=
x3;(2)当t=1时,S△PBQ最大=![]() .;(3)当t的值是
.;(3)当t的值是![]() 秒或
秒或![]() 秒或
秒或![]() 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.
【解析】(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=-![]() (t-1)2+
(t-1)2+![]() .利用二次函数的图象性质进行解答;
.利用二次函数的图象性质进行解答;
(3)分为三种情况:①当PB=BQ,②当PQ=BQ,③当PQ=PB进行讨论,
(1)把点A(2,0)、B(4,0)分别代入y=ax2+bx3(a≠0),得
![]()
解得a=![]() ,b=
,b=![]()
所以该抛物线的表达式式为:y=![]() x2
x2![]() x3
x3
(2)由题意可知:AP=3t,BQ=t.
∴PB=63t.
由题意得,点C的坐标为(0,3).
在Rt△BOC中,BC=![]() .
.
如图1,过点Q作QH⊥AB于点H.
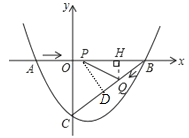
∴QH∥CO,
∴△BHQ∽△BOC
∴![]() ,即
,即![]()
∴HQ=![]() t.
t.
∴S△PBQ=![]() PBHQ=
PBHQ=![]() (63t)
(63t) ![]() t=
t=![]() t2+
t2+![]()
t=![]() (t1)2+
(t1)2+![]() .
.
∴当t=1时,S△PBQ最大=![]() . ()
. ()
答:运动1秒使△PBQ的面积最大,最大面积是![]() ;
;
(3)分为三种情况:①当PB=BQ时,即63t=t,解得t=![]()
当t=![]() 秒,△BPQ是等腰三角形。
秒,△BPQ是等腰三角形。
②当PQ=BQ时,
∵QH⊥PB,
∴PH=BH=![]() (63t)=3
(63t)=3![]() t,
t,
∵cos∠HBQ=![]()
∴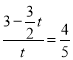 ,解得t=
,解得t=![]()
∴当t=![]() 秒时,△BPQ是等腰三角形,
秒时,△BPQ是等腰三角形,
③当PQ=PB时,如图,过P点作PD⊥BC
∵PD⊥BC,
∴BD=QD=![]() BQ=
BQ=![]() t,
t,
∵cos∠HBQ=![]()
∴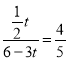 ,解得t=
,解得t=![]()
∴当t=![]() 秒时,△CPQ是等腰三角形,
秒时,△CPQ是等腰三角形,
即当△CPQ为等腰三角形时,t的值是![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
(1)求证:BD平分∠PBC;
(2)若PD =3DE,求
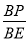 的值.
的值.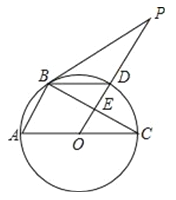
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,OA =10,sin∠AOB =
 ,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.
,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.(1)求反比例函数的表达式;
(2)若点F为BC的中点,求△OBF的面积.
-
科目: 来源: 题型:
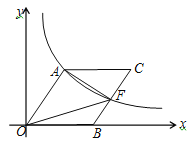
查看答案和解析>>【题目】阅读理解:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.垂美四边形有如下性质:
垂美四边形的两组对边的平方和相等.
已知:如图1,四边形ABCD是垂美四边形,对角线AC、BD相交于点E.
求证:AD2+BC2=AB2+CD2
证明:∵四边形ABCD是垂美四边形
∴AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2.
拓展探究:
(1)如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
问题解决:
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5.求GE长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从圆形跑道(圆形跑道的总长小于700m)上一直径两端A,B相向起跑.第一次相遇时离A点100m,第二次相遇时离B点60m,则圆形跑道的总长为( )
A.240mB.360mC.480mD.600m
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-12a2b2c)·(-
 abc2)2;
abc2)2;(2)(3a2b-4ab2-5ab-1)·(-2ab2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于10的概率.
相关试题

