搜索
【题目】某多边形的内角和是其外角和的3倍，则此多边形的边数是（ ）
A. 8 B. 7 C. 6 D. 5
参考答案：
【答案】A
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF．连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．
（1）请判断：FG与CE的数量关系是 ，位置关系是 ；
（2）如图2，若点E，F分别是边CB，BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请作出判断并给予证明；
（3）如图3，若点E，F分别是边BC，AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
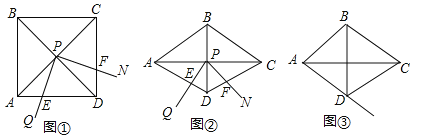
（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是 ；
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=
AD，请给出证明；（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：如图（1），在Rt△ACB中，∠ACB=90°，AC=CB，∠DCE=45°，试探究AD、DE、EB满足的等量关系．
[探究发现]
小聪同学利用图形变换，将△CAD绕点C逆时针旋转90°得到△CBH，连接EH，由已知条件易得∠EBH=90°，∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°．根据“边角边”，可证△CEH≌ ，得EH=ED．
在Rt△HBE中，由 定理，可得BH2+EB2=EH2，由BH=AD，可得AD、DE、EB之间的等量关系是 ．
[实践运用]
（1）如图（2），在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数；
（2）在（1）条件下，连接BD，分别交AE、AF于点M、N，若BE=2，DF=3，BM=2
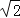，运用小聪同学探究的结论，求正方形的边长及MN的长．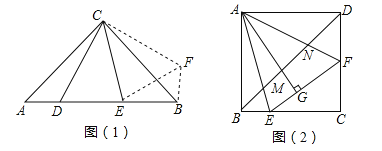
-
科目： 来源： 题型：
查看答案和解析>>【题目】在频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其它10个小长方形面积的和的
，且数据有160个，则中间一组的频数为（ ）
A.32
B.0.2
C.40
D.0.25 -
科目： 来源： 题型：
查看答案和解析>>【题目】如果单项式x2ym+2与xny的和仍然是一个单项式，则(m+n)2019等于( )
A. 1 B. ﹣1 C. 2019 D. ﹣2019
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于平行四边形ABCD的叙述，正确的是( )
A. 若AB⊥BC，则平行四边形ABCD是菱形 B. 若AC⊥BD，则平行四边形ABCD是正方形
C. 若AC=BD，则平行四边形ABCD是矩形 D. 若AB=AD,则平行四边形ABCD是正方形
相关试题
