【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
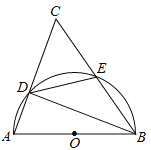
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
参考答案:
【答案】(1)等腰三角形;(2)![]()
【解析】
试题分析:根据AB是直径,则我们很容易知道![]() ,同时也是
,同时也是![]() .进而就有
.进而就有
![]() ,而又
,而又![]() ,则DE=BE,进而
,则DE=BE,进而![]() ,所以
,所以![]() ,而ABED可以看成是个圆内接四边形,则
,而ABED可以看成是个圆内接四边形,则![]() ,所以
,所以![]() ,即⊿ABC为等腰三角形.
,即⊿ABC为等腰三角形.
第(2)问要求的是![]() 的正弦值,由图知,
的正弦值,由图知,![]() 在
在![]() 中,AB=10,要求正弦值,就必须求得AD的值,在
中,AB=10,要求正弦值,就必须求得AD的值,在![]() 中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出
中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出![]() .
.
试题解析:(1)∵AB为直径,
∴∠ADC=∠BDE=90°,∠C+∠DBC=90°,∠CDE+∠EDB=90°,
又∵![]() ,
,
∴∠EDB=∠DBC,
∴∠C=∠CDE,
∴CE=DE,
∵![]() ,
,
∴DE=BE,CE=BE,
∴AE垂直平分BC,
∴AC=BC,
∴△ABC为等腰三角形.
∵A,B,E,D四点共圆,
∴∠CDE=∠CBA,∠C公用,
∴△CDE∽△CBA,
∴![]()
∵BC=12,半径为5,
由(1)得AC=BC=10,CE=6,
即![]()
解得CD=7.2,
∴AD=AC-CD=2.8;
∴sin∠ABD=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块直角三角形纸板如图①摆放,
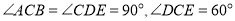 ,现将
,现将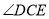 绕
绕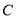 点逆时针转动;
点逆时针转动;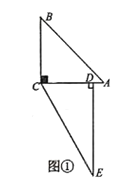
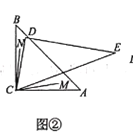
 当转动至图②位置时,若
当转动至图②位置时,若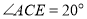 ,且
,且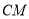 平分
平分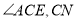 平分
平分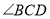 ,则
,则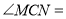 _;
_;
 当转动至图③位置时,
当转动至图③位置时,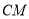 平分
平分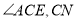 平分
平分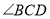 ,求
,求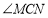 的度数;
的度数;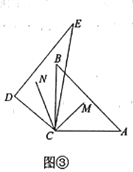
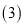 当转动至图④位置时,
当转动至图④位置时,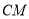 平分
平分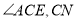 平分
平分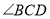 ,请直接写出
,请直接写出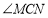 的度数.
的度数.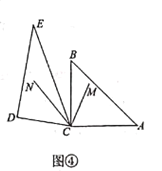
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点
 分别对应数
分别对应数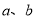 ,其中
,其中 .
.
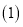 当
当 时,线段
时,线段 的中点对应的数是_ _____ .(直接填结果)
的中点对应的数是_ _____ .(直接填结果) 若该数轴上另有一点
若该数轴上另有一点 对应着数
对应着数 .
.①当
 ,且
,且 时,求代数式
时,求代数式 的值:
的值:②
 .且
.且 时学生小朋通过演算发现代数式
时学生小朋通过演算发现代数式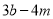 是一个定值
是一个定值老师点评:小朋同学的演算发现还不完整!
请你通过演算解释为什么“小朋的演算发现”是不完整的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(
 ,y1),B(
,y1),B( ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“
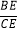 =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).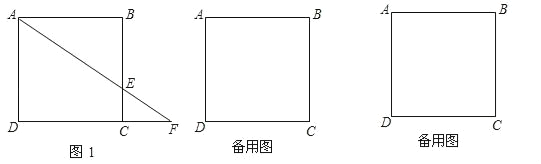
相关试题

