【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小.
参考答案:
【答案】(1) 顶点坐标是(1,4),对称轴为直线x=1;(2) y1>y2.
【解析】分析:(1)将a、b的值代入函数解析式即可;
(2)根据(1)中的结论,即可求得m的值;
(3)根据题意和二次函数的性质,利用分类讨论的数学思想即可求得y1与y2的大小.
详解:(1)当a=-2,b=-4时,
y=-2x2+4x+2=-2(x-1)2+4,
∴该函数图象的顶点坐标是(1,4),对称轴为直线x=1;
(2)点Q(m,t)关于原点对称的点的坐标P是(-m,-t),
则![]() ,
,
解得,m=±1;
(3)∵函数的图象经过点(1,0),
∴0=a-b+2,
∴b=a+2,
∵y=ax2-bx+2,
∴函数的对称轴为直线x=![]() ,
,
当a>0时,![]() <
<![]() +
+![]() <
<![]() +
+![]() ,
,
∵![]() +
+![]() -
-![]() =
=![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=
)=![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y2>y1,
当a<0时,![]() +
+![]() <
<![]() +
+![]() <
<![]() ,
,
∵![]() -(
-(![]() +
+![]() )=-
)=-![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=-
)=-![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块直角三角形纸板如图①摆放,
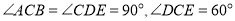 ,现将
,现将 绕
绕 点逆时针转动;
点逆时针转动;
 当转动至图②位置时,若
当转动至图②位置时,若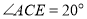 ,且
,且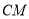 平分
平分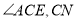 平分
平分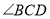 ,则
,则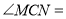 _;
_;
 当转动至图③位置时,
当转动至图③位置时,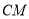 平分
平分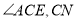 平分
平分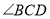 ,求
,求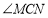 的度数;
的度数;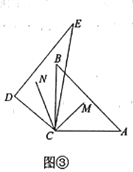
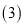 当转动至图④位置时,
当转动至图④位置时,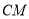 平分
平分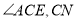 平分
平分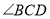 ,请直接写出
,请直接写出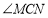 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且
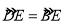 .
.
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求
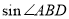 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点
 分别对应数
分别对应数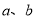 ,其中
,其中 .
.
 当
当 时,线段
时,线段 的中点对应的数是_ _____ .(直接填结果)
的中点对应的数是_ _____ .(直接填结果) 若该数轴上另有一点
若该数轴上另有一点 对应着数
对应着数 .
.①当
 ,且
,且 时,求代数式
时,求代数式 的值:
的值:②
 .且
.且 时学生小朋通过演算发现代数式
时学生小朋通过演算发现代数式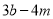 是一个定值
是一个定值老师点评:小朋同学的演算发现还不完整!
请你通过演算解释为什么“小朋的演算发现”是不完整的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“
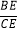 =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
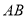 、
、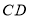 相交于
相交于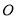 ,∠EOC=90°,
,∠EOC=90°,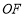 是
是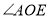 的角平分线,
的角平分线, ,求
,求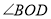 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.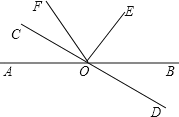
解:∵

 ( )
( )∴
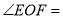
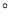
∵
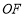 是
是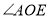 的角平分线
的角平分线∴
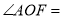
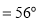 ( )
( )∴
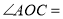
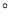
∵
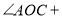
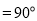
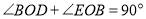 ( )
( )∴
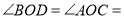
 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图,下列说法中,错误的是
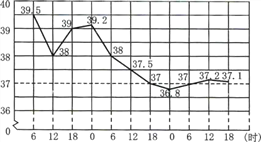
①护士每隔6小时给病人量一次体温;
②这个病人的体温最高是39.5摄氏度,最低36.8摄氏度;
③他的体温在4月9日18时到4月10日18时比较稳定;
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
相关试题

